MSC.adams軟件在汽車空調壓縮機中的應用

引言

　　隨著人們生活水平的提高，對汽車舒適性的要求也越來越高。汽車空調的質量影響到對整車的評價。由于汽車是直接暴露在太陽或風雪下，而且汽車行駛的速度變化無常，車內的空間有限。這都加大了汽車空調的設計難度。一般來說汽車空調由壓縮機，冷凝器，蒸發器，和膨脹閥組成。汽車空調壓縮機是汽車空調的關鍵零部件，也是主要的運動部件。采用虛擬樣機技術可以研究汽車空調壓縮機的運動規律和動力性能，為設計和優化提供幫助。

　　虛擬樣機技術是在產品的設計開發中，將分散的零部件設計和分析技術融合在一起，在計算機上建造出產品的整體模型，并對該產品在投入使用后的各種工況進行仿真分析，預測產品的整體性能，進而改進設計，提高產品質量。

　　本文是采用MSC.ADAMS 軟件對一款汽車空調壓縮機進行運動，動力分析，從而了解其運動規律，并計算一些聯接副的受力情況。

　　1 汽車空調壓縮機運動機構概述

　　汽車空調壓縮機可分為往復式和旋轉式二大類。往復式的又分曲軸連桿式，軸向活塞式，和徑向活塞式。其中軸向活塞式又分旋轉斜盤式和搖擺斜盤式。旋轉式又分刮片式，滾動活塞式，三角轉子式，渦旋式，螺桿式。本文主要研究5 缸搖擺斜盤式的汽車空調壓縮機。

　　搖擺斜盤式的汽車空調壓縮機的工作原理是通過主軸的旋轉帶動斜盤的轉動，通過只能進行擺動的行星盤將旋轉運動轉化為活塞的往復運動，活塞在氣缸里對制冷劑進行壓縮。(見圖1)

　　圖1 空調壓縮機核心部件裝配圖

　　2 搖擺斜盤式壓縮機運動學幾何關系

　　搖擺斜盤式壓縮機通過主軸帶動斜盤作圓周運動，行星盤由于導向桿的運動約束，將主軸的周轉運動轉化為斜盤表面質點的軸向往復，并通過連桿帶動活塞，構成空間上類曲柄滑塊機構。

　　本模型中，由于受到行星盤上導向桿的約束，活塞3 的連桿連接行星盤一端的球心始終位于軸線與導向桿軸線所確定的平面內，該活塞的運動處于較為特殊的地位，幾何關系為平面運動。其余活塞1，5，活塞2，4 互為對等關系，且均屬空間運動學范疇。

　　3 活塞運動學公式推導

　　在研究壓縮機時，活塞的運動規律十分重要。下面以活塞3 為例，對壓縮機的活塞質心運動進行公式推導。

　　如圖2 所示，對該幾何關系構建封閉矢量多邊形，l1、l2、l3、s4 均為相應的桿矢量，θ1、θ2、θ3、θ4 為桿件的方位角，各桿件矢量方向不影響計算結果，但方位角均應由x 軸開始，并以沿逆時針方向計量為正。

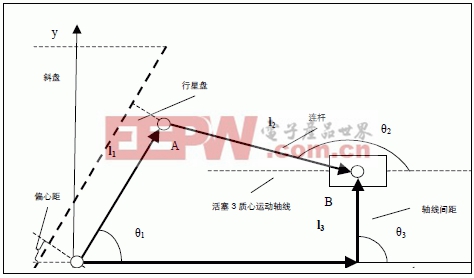
　　圖2 活塞3 運動幾何關系

　　由于主軸軸線(即斜盤軸線)和行星盤軸線各自在工作結合面(粗虛線)上的交點有一偏心距，其偏置的結果正好使得行星盤中心球狀腔的球心(O 點)落在了主軸軸線(X 軸)上。

　　所以，在固定球輪的頂壓下，行星盤完全繞O 點作擺動，行星盤中心孔腔的球心(O 點)到圓周孔腔(即連桿球鉸鏈落位處)的球心(A 點)之間的距離為曲柄長度，連桿兩球心之間距離為連桿長度，活塞質心運動狀態等效B 點(球鉸鏈球心)運動狀態。

　　由于在封閉矢量多邊形中，各矢量之和為零：

　　4 通過MSC.ADAMS 對壓縮機進行運動動力分析

　　4.1 分析的基本步驟

　　汽車空調壓縮機的仿真過程如下：1. 運用UG 的三維實體建模模塊對壓縮機核心運動機構進行三維建模，主要包括主軸、斜盤、行星盤、連桿和活塞五大部件，并在UG 環境下進行裝配。2. 將建好的實體模型以Parasolid 格式輸出，導入ADAMS 中，添加材料屬性，并根據默認位置關系附加運動約束，實現模擬運動無干涉。3. 根據三種給定的不同工況，計算活塞端面的氣體壓力，將氣體力學方程導入，完成力學約束的添加。4. 根據工況，在驅動軸上賦給指定轉速，輸出動力學特性曲線，包括活塞質心位移曲線、活塞質心速度曲線、活塞質心加速度曲線和活塞端面力曲線。并對獲取的數據進行動力學分析。

　　4.2 零部件的物理參數

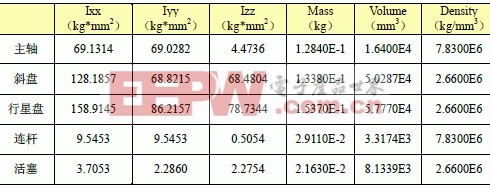
　　其幾何參數和慣性參數采用三維CAD 實體建模軟件UG-Ⅱ計算得到，如表1 所示。這對幾何形狀極不規則，采用計算方法很難得到準確數值的物體，如斜盤等，將大大簡化計算過程。

　　表1 空調壓縮核心部件力學參數

　　4.3 約束的選定

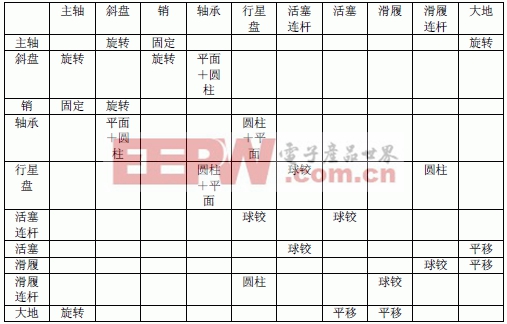
　　在ADAMS 的VIEW 模塊對模型中的零件之間的運動副進行約束定義。下表為運動副的約束定義。

　　表2 空調壓縮核心部件運動約束

　　4.4 確定邊界條件(活塞壓力的確定)

　　4.4.1 仿真工況：

　　按試驗要求，如表4.2.3-1 所示，仿真過程將在900rps、5500rps、7000rps 三種轉速及各自相對應的吸氣壓強、排氣壓強下進行測試。

　　表3 空調壓縮機試驗工況

　　4.4.2 活塞頂部壓力公式推導：

　　根據氣體方程：多變過程的 P*VN=C 得出：

　　壓縮過程：P1=Ps*((L+C)/( .5H11G.cm_dis+d3+C)) N

　　排氣過程：P2=Pd

　　膨脹過程：P3=Pd*(C/(.5H11G.cm_dis+d3+C)) N

　　吸氣過程：P4=Ps

　　其中：

　　L=壓縮機平均行程

　　C=余隙

　　N=多變指數

　　d3=活塞下止點平均位置

　　.5H11G.cm_dis=活塞質心點位置