無(wú)重疊生成文法的一義可解析性及圖林等價(jià)性

2 定義
定義2．1一個(gè)無(wú)重疊生成文法(簡(jiǎn)稱(chēng)0FG)是一個(gè)系統(tǒng)式中：N和T分別是非終止符和終止符集合，S是啟始符，它是N的一個(gè)元素，$是限界符，它不屬于上面任何一個(gè)集合，P是重寫(xiě)規(guī)則的集合，其中任一重寫(xiě)規(guī)則具有：

這里α，β∈(N∪T)，α≠β，A∈N，且每個(gè)規(guī)則滿(mǎn)足下列條件：
重寫(xiě)規(guī)則的左部至少有一個(gè)非終結(jié)符，其右部不能是$5，S$,$S$或S。
對(duì)任意兩個(gè)重寫(xiě)規(guī)則r1=α1→β1和r2=α2→β2，應(yīng)滿(mǎn)足：①不存在δ，β′1,β'2∈(N∪T∪{$})+使得β1=β′1δ和β2=δβ′2，即β1和β2不能有任何相互重疊的部分；②如果存在γ，γ′∈(N∪T∪{$}){$})*使β1=γβ2γ'，則r1=r2。
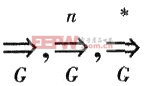令η∈{N∪T)+,α→β是P中的任意一個(gè)規(guī)則，如果存在γ，δ∈(N∪T∪{$})*，使得η=γaδ，則稱(chēng)規(guī)則α→β可應(yīng)用于η。通過(guò)對(duì)η應(yīng)用規(guī)則α→β，可以得到ζ=γβδ,對(duì)此，稱(chēng)在G中ζ可由應(yīng)用規(guī)則α→β從η直接推導(dǎo)而得，記為，或簡(jiǎn)記為的自反傳遞閉包記為如果存在ξ1，ξ2，…，ξn-1使得，則記為在G為默認(rèn)的情況下，分別簡(jiǎn)記為
令η∈(N∪T)+，若為G中的一個(gè)推導(dǎo)句型，稱(chēng)η為G中的一個(gè)句型。對(duì)于任一文法G，其生成的語(yǔ)言定義為：

定義2．2一個(gè)確定性圖靈機(jī)(簡(jiǎn)稱(chēng)DTM)是一個(gè)系統(tǒng)M：

式中：Q是狀態(tài)集合，∑是輸入符號(hào)的集合，Г帶符號(hào)集合，是一個(gè)移動(dòng)函數(shù)，a0∈Г是一個(gè)空白符號(hào)，q0是初始狀態(tài)，qf是終止?fàn)顟B(tài)。
假設(shè)M具有一個(gè)向右無(wú)限的符號(hào)帶，M總是從符號(hào)帶的最左端位置以初始狀態(tài)開(kāi)始移動(dòng)讀寫(xiě)頭，且讀寫(xiě)頭右側(cè)永不存在不連續(xù)字符帶(圖林機(jī)在任何時(shí)候都不向連續(xù)字符帶的中間寫(xiě)空白字符，只能在最右端寫(xiě)空白字符)。這樣的假設(shè)并不影響M的通用性。
定義2.3設(shè)C是一類(lèi)文法系統(tǒng)或一類(lèi)圖靈機(jī)，L[C]表示該類(lèi)系統(tǒng)所生成或接受的語(yǔ)言的集合，稱(chēng)為C的語(yǔ)言類(lèi)，即：
L[C]={L(G)|G∈C}

3 圖靈通用性
引理3．1 OFG所生產(chǎn)的語(yǔ)言類(lèi)是DTM接受的語(yǔ)言類(lèi)的子集，即

證明：很顯然，對(duì)任何一個(gè)0FG文法G均可以容易地構(gòu)造一個(gè)等價(jià)的Cllomsky O型文法G′，故O型文法]。而三L[Cllomsky 0型文法]=L[DMT]。或簡(jiǎn)單地說(shuō)，L[OFG]是遞歸可枚舉集的子集。
引理3．2 DTM接受的語(yǔ)言類(lèi)是0FG所生產(chǎn)的語(yǔ)言類(lèi)的子集，即：

證明：可以用0FG來(lái)模擬任一個(gè)確定的圖靈機(jī)的逆過(guò)程。不失一般性，假設(shè)圖靈機(jī)具有右無(wú)窮長(zhǎng)帶，且在任何狀態(tài)下具有連續(xù)的字符序列，在任何時(shí)候都不向字符帶中段上寫(xiě)空白字符。