利用重疊掃描方法改進單片機乘法運算
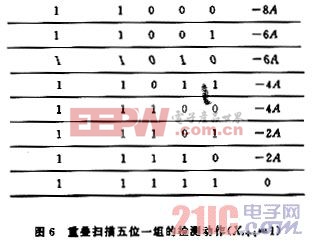
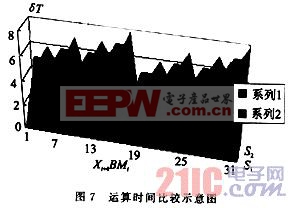
區別只是改加為減,因為部分積的減值在以后的掃描中可以修正回來,不用采用補碼的運算也能完成,最常用的方法是設置輔助運算區,采用臨時記錄的方式保證其部分積在掃描任一周期保持正確結果,也稱為臨時擴展方法,這里就不重復。這樣,在每次掃描僅剩下一個問題,即如何處理Pj,這里Pj與文[3]中處理的方法有類似之處。以2A為基礎,將Pj形成一個加(減)法序列,也就是將Pj變為2qA的序列,如12A=22A+23A。這樣就可以在一個掃描周期完成部分積的加法。這里建議讀者去探索Pj更好的形成方法,因為形成2qA的序列,1≤q≤3,要占用時間(24A可以通過半字節操作做左端拼加處理,因為24A相當于A左移半字節,運算時直接依靠輔助運算區),同時在特殊處理上也額外占有一些運算時間,這一點在圖7中也可以看出來。這樣一來,在Pj的加法過程中,掃描算法在某些BMi值上并不都占優勢,這一點在圖5,6中也可以體現(BMi中Xi+3,Xi+2,Xi+1,Xi為1的個數決定了在標準算法中的加法次數);但重疊掃描畢竟節省了時間,其與標準算法在一個掃描周期內的加法次數情況如圖8所示(其中系列1為重疊掃描算法,系列2為標準算法)。加之在移位中節省的時間,重疊掃描全過程的運算時間與標準右移算法的比較情況如圖8所示(S1為重疊掃描算法,S2為標準算法)。在局部區域,由于采用上述的Pj處理方法,運算時間節省情況還不甚理想,但在總體上還是有很大的改進。

4 結 論
以上介紹的是重疊均勻移位掃描算法,前面談到重疊非均勻移位掃描算法,有關這種算法的詳細介紹請參見其他文獻。
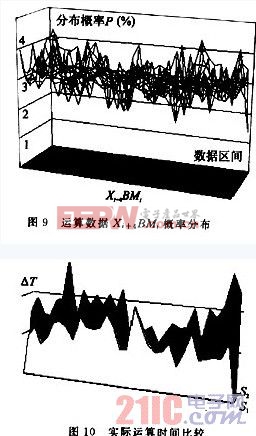
在以上過程中,是假定BMi中的Xi+3,Xi+2,Xi+1,Xi值的1,0分布服從自然概率,然而在運算中由于Xi+4的作用,在對某區間數據進行操作時存在差異,通過對一些運算區間的數據進行了統計,其Xi+4與BMi值的分布概率如圖9所示;以實際的一組分布來驗證重疊算法運算時間的縮短情況,如圖10所示(S1為重疊掃描算法,S2為標準算法;圖中前面為S1,后面陰影為S2)。可以看到重疊掃描法對浮點多字節乘法運算有很大的改進,它打破了移位加法的傳統乘法算法,有了算法的預測功能,提高了乘法運算的速度。本算法在某軍工項目中得到應用,效果很好。
參考文獻
1 黃 凱.計算機算術運算原理、結構與設計.北京:科學出版社,1980.106~110
2 陳 宇,王遵立.MC-51單片微型機上實現的快速掃描浮點乘法運算.數據采集與處理,1992,(9):151~153
3 陳 宇,畢淑艷,王遵立,等.MCS-51單片機實現的快速浮點多字節BCD乘除運算.電子技術應用,1998,(2):17~19
4 Chen T C.A binary multiplication scheme based onsquaring.IEEE Trans Comput,1971,C-20(6):678~680
5 Booth A D.A signed binary multiplication technique.Quart Journ Mech and Appl,Math,1951,4(2):236~240
6 Garner H L.A ring model for the study for a binarymultiplier using 2,3 or 4-bit at a time.IEEE Trans,1959,EC-80(1):25~30











評論