基于SOPC的高精度超聲波雷達測距系統設計

摘要：本文基于NIOS II軟核處理器和卡爾曼濾波算法，利用FPGA平臺，超聲波傳感器和LCD液晶顯示系統，設計了一種高精度超聲波雷達測距系統。以這種方法設計的SOPC系統，克服了傳統超聲波雷達測距系統噪聲干擾過大的問題，提高了測距系統的測量精度。

引言

　　傳統的超聲波雷達測距系統面臨噪聲過大、測量精度不夠高的問題，卡爾曼濾波算法是一種最優化自回歸數據處理算法，在雷達測距和目標跟蹤等領域有廣泛應用，可以用來提高測距系統的精度。但是卡爾曼濾波算法的實現需要用到大量的浮點數矩陣運算，軟件實現方式通常很難滿足系統對于高實時性的要求，硬件雖然可以保證系統的高實時性，但是硬件無法直接處理浮點數，并且硬件開發周期過長，成本過高，這都限制了卡爾曼濾波算法的應用。

　　NIOS II處理器是可編程邏輯器件的軟核處理器，可以和存儲器、I/O接口等外設嵌入到FPGA中，組成一個靈活、高效的可編程單芯片系統(SOPC)，大大降低了系統的成本、體積和功耗，適合網絡、電信、數據通信、嵌入式和消費市場等各種嵌入式應用場合^[1-3]。

　　本文基于FPGA平臺，采用NIOS II軟核處理器，利用卡爾曼濾波算法對系統測量值進行濾波處理，設計了一種SOPC系統，以這種方法設計的測距系統綜合利用了軟件編程靈活的優點以及硬件并行處理、速度較快的特點，運用軟硬件協同設計方法保證系統的整體性能最優^[4]，從而大大提高了測距系統的性能和精度。

1 卡爾曼濾波理論

　　對于卡爾曼濾波器，首先我們需要引入一個系統方程：

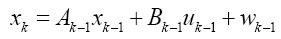
　　系統的測量方程為：

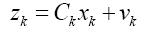
　　對于系統方程，矩陣A稱為轉換矩陣，矩陣B稱為控制矩陣，矩陣C稱為測量矩陣，u是控制量，A、B、C、u由實際濾波模型決定，均為已知，上述參數可以是恒定的，也可以是隨時間變化的^[5]。w是系統噪聲，v是測量噪聲。

　　卡爾曼濾波算法由五條濾波公式組成：

　　公式一：狀態預測方程

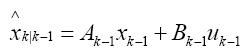
　　公式二：誤差預測方程

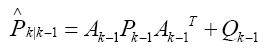
　　公式三：卡爾曼增益方程

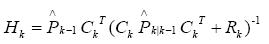
　　公式四：濾波估計方程

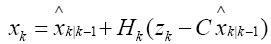
　　公式五：誤差更新方程

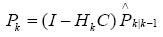
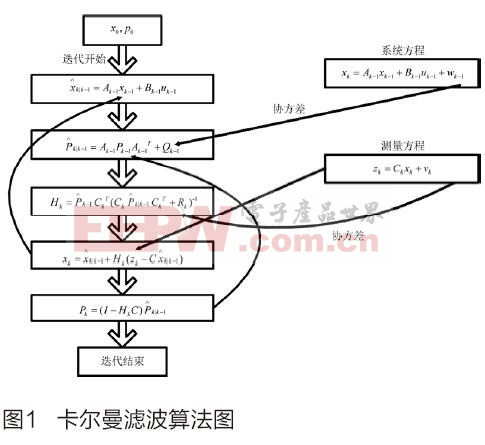
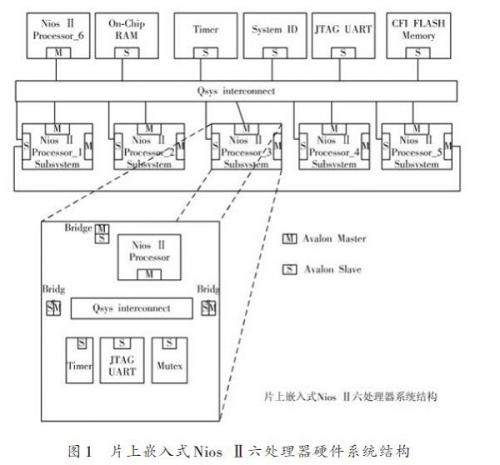
　　卡爾曼濾波算法如圖1所示。濾波算法用反饋控制的方法估計過程狀態，濾波器首先預測過程某一時刻的狀態，然后通過測量值對預測值進行反饋和校正，其中公式一和公式二組成預測方程，產生先驗估計，公式三、公式四和公式五組成校正方程，將先驗估計和測量值結合構造改進的后驗估計，即用測量值對預測值進行校正，卡爾曼濾波器就是通過這樣一個不斷的“預測(先驗)—測量—校正(后驗)”的過程，使得最優估計的誤差隨時間以指數衰減，從而使得數據逐漸“收斂”，以此來達濾波的目的^[6 。

2 系統硬件設計

　　如圖2所示，系統的硬件部分由超聲波傳感器，FPGA開發板以及LCD液晶屏組成。系統工作時，FPGA通過超聲波傳感器的驅動模塊來讀取傳感器采集的實時測量數據，這些數據經過卡爾曼濾波算法進行濾波和去噪處理后，再通過LCD驅動模塊控制LCD液晶屏進行數據的實時展示。

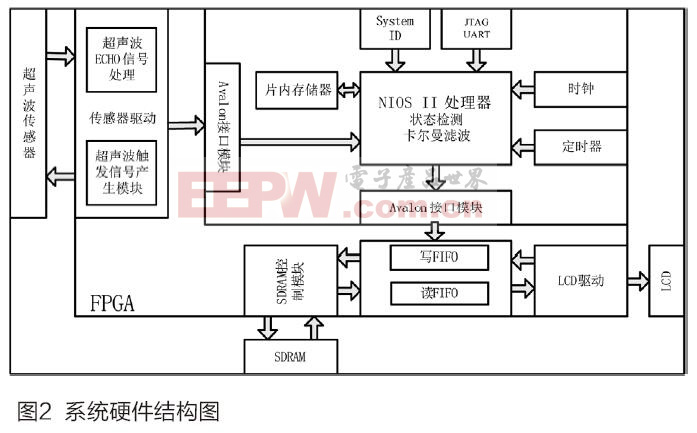
　　在該系統中，超聲波傳感器驅動和LCD驅動采用Verilog HDL設計，卡爾曼濾波模塊通過NIOS II軟核中的C語言實現。這樣既可以發揮硬件處理速度快的特點，又可以很好的發揮C語言處理浮點數運算和編程靈活的特點，從而保證系統性能最優。

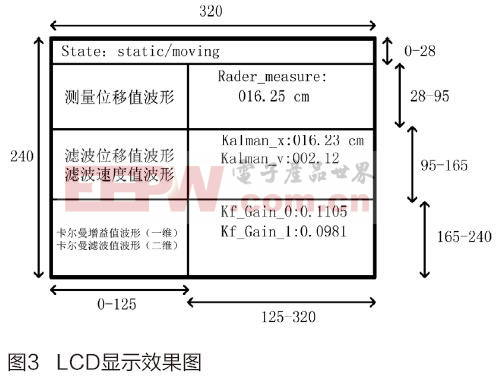
　　系統采用的LCD液晶屏的尺寸是320*240。圖3是LCD屏幕的分區顯示效果圖，液晶屏最上部顯示運動狀態檢測結果，下部顯示實時數據，其中左側顯示實時波形曲線，右側顯示實時數值數據。

3 系統軟件設計

　　該系統的軟件算法流程如圖4所示，FPGA通過超聲波傳感器采集距離信息，并進行距離信息的存儲以完成被檢測物體的運動狀態判斷，當物體處于靜止狀態時則使用一維卡爾曼濾波算法對含噪聲的距離測量值進行濾波去噪;當物體處于運動狀態時，則使用二維卡爾曼濾波算法對含噪聲的距離測量值進行去噪和優化處理，并可以利用關系矩陣和濾波算法得到運動物體的速度值。