一文搞懂《擴展卡爾曼濾波融合IMU和ODOM》
x)。但狙擊手看不到這些 “真實值”,只能通過瞄準鏡(傳感器)得到帶誤差的觀測(比如 “好像在 100 米處,可能偏左半米”)。觀測數據里的 “噪聲和干擾”,就像瞄準鏡前的樹葉、霧氣、樹木遮擋
當樹葉擋住視線時(觀測數據突然不準),卡爾曼濾波不會完全相信這一幀的觀測,而是更多依賴 “基于目標運動規律的預判”(比如 “剛才目標在勻速跑,不可能突然跳 10 米,這幀數據肯定是被樹葉擋了,忽略它”)。

擴展卡爾曼濾波(EKF)是卡爾曼濾波(KF)的 “升級版”,專門用來解決卡爾曼濾波搞不定的場景。我們可以繼續用 “狙擊槍瞄準移動靶” 的比喻來理解它們的關系:
1. 卡爾曼濾波(KF):只能對付 “規矩的目標”
卡爾曼濾波的核心前提是:目標的運動規律是 “線性的”。
比如移動靶在勻速直線運動(速度不變、方向不變),或者勻加速運動(每秒多跑 1m/s)—— 這些運動可以用簡單的線性公式描述(比如 “下一秒位置 = 現在位置 + 速度 × 時間”)。
這時候,狙擊手只要用 “勻速 / 勻加速模型” 就能精準預判,卡爾曼濾波的公式也能直接套用,計算簡單又高效。
2. 擴展卡爾曼濾波(EKF):能搞定 “調皮的目標”
但現實中,很多目標的運動是 “非線性的”:
比如移動靶突然轉彎、繞圈,甚至做 S 形走位(運動方向和速度的關系不是簡單的線性公式);
或者傳感器的觀測方式是非線性的(比如用雷達測角度,角度和位置的關系是三角函數,不是直線關系)。
它會在 “當前估計的狀態點” 附近,用一條直線(切線)近似目標的非線性運動軌跡(就像用很多小線段拼接成曲線)。這樣一來,就能繼續套用卡爾曼濾波的線性公式來計算,只不過每次都要重新算這條 “切線”(專業上叫 “線性化”,用雅克比矩陣實現)。
總結:關系就像 “基礎款計算器” 和 “科學計算器”
卡爾曼濾波是 “基礎款”:只能算加減乘除(線性問題),簡單直接,速度快。 擴展卡爾曼濾波是 “科學計算器”:能處理三角函數、指數等復雜運算(非線性問題),通過 “近似線性化” 擴展了適用范圍,但計算更復雜一點。 兩者的核心邏輯(“預判 + 修正” 的濾波思想)完全一致,只是 EKF 能應對更貼近現實的非線性場景。
咱們可以把 EKF 融合 IMU 和 ODOM 的過程,想象成一個 “猜位置” 的游戲,你需要結合兩種 “線索” 來不斷修正自己的猜測,讓結果越來越準。
IMU(Inertial Measurement Unit)和 ODOM(Odometry)在機器人領域以及其他涉及運動感知和定位的系統中是非常重要的概念,以下是它們的詳細介紹:
IMU(慣性測量單元)
定義
IMU 是一種能夠測量物體三軸加速度和三軸角速度的組合式傳感器,有的 IMU 還集成了磁力計 ,可以測量物體的磁場信息,輔助確定物體的方向。它是一個小型化、高度集成的系統,能夠實時提供物體的運動狀態信息。 工作原理
加速度計
:基于牛頓第二定律,通過檢測內部質量塊在加速度作用下產生的力,來測量加速度。比如,當物體加速時,質量塊會相對于傳感器內部的固定結構產生位移,通過檢測這種位移并將其轉換為電信號,就可以得到加速度的大小和方向。 陀螺儀
:利用科里奧利力原理工作。當陀螺儀的殼體發生旋轉時,內部的旋轉質量塊會受到科里奧利力的作用,從而產生微小的振動或偏移,通過檢測這些變化就可以測量出角速度。
ODOM(里程計)
定義
里程計是一種用于測量物體在運動過程中移動距離和方向的裝置或算法,通過對運動過程中的一些參數進行累計和計算,來確定物體的位置變化。 工作原理
輪式里程計
:常見于輪式機器人,通過安裝在輪子上的編碼器來記錄輪子的轉動圈數。結合輪子的半徑,就可以計算出機器人在平面上移動的距離。同時,通過一些額外的傳感器(如安裝在差速驅動機器人兩個輪子上的編碼器,對比兩個輪子的轉動圈數差異),可以推算出機器人的轉向角度和方向變化。
先給兩個 “線索源” 做個簡單畫像:
IMU:像你身上的 “運動傳感器”,能實時感覺到自己在怎么動 —— 比如走得快還是慢、有沒有轉彎(用角速度測轉彎,用加速度測加速)。但它有個毛病:猜多了會 “跑偏”(比如站著不動,它可能會慢慢覺得你在挪位置,這叫 “漂移”)。
ODOM:像你手里的 “路標導航”,每隔一會兒告訴你當前的位置和速度(比如輪式里程計通過輪子轉了多少圈算位置,或者視覺里程計通過攝像頭看環境算位置)。它相對穩定,不會輕易跑偏,但更新沒那么快(比如輪子轉半圈才出一次數據),而且偶爾會 “騙你”(比如輪子打滑時,它算的位置就不準了)。
EKF 做的事,就是用 IMU 的 “實時感覺” 先“猜”,再用 ODOM 的 “路標信息” 來修正,最后得到一個又快又準的結果。具體分兩步:
第一步:用 IMU “猜”(預測階段)
假設你現在要走路去超市,EKF 先根據 IMU 的信息,實時猜你每一秒的位置和速度。比如:
上一秒你在 “小區門口”(上一時刻的位置),速度是 “1 米 / 秒向前”(上一時刻的速度)。
這一秒 IMU 告訴你:“你沒轉彎(角速度為 0),也沒加速(加速度為 0)”(IMU 的測量值)。
那 EKF 就會猜:“這一秒你應該在小區門口往前 1 米的地方,速度還是 1 米 / 秒”(預測的當前位置和速度)。
但 EKF 知道 IMU 會 “跑偏”,所以猜的時候會留個 “誤差范圍”:比如 “位置大概在 1 米左右,誤差可能有 0.5 米”(這個誤差會隨著 IMU 用得越久慢慢變大,就像猜多了越來越沒譜)。
第二步:用 ODOM “修正”(更新階段)
走了一會兒,ODOM 這個 “路標” 說話了:“根據輪子轉的圈數,你現在應該在‘離小區門口 1.2 米’的地方”(ODOM 的測量值)。
這時候 EKF 要做兩件事:
對比 “猜的位置(1 米)” 和 “ODOM 說的位置(1.2 米)”,算出差了 0.2 米。
看看這兩個線索誰更可信,再決定怎么修正。
比如:
如果地面很平,輪子沒打滑,ODOM 很靠譜(權重高),那就多聽 ODOM 的,把猜測從 1 米調成 1.15 米(靠近 1.2 米)。
如果地面坑坑洼洼,輪子可能打滑了,ODOM 不太準(權重低),就少聽 ODOM 的,調成 1.05 米(靠近原來的猜測)。
循環往復,越猜越準
之后就重復這兩步:
沒 ODOM 數據時,用 IMU 實時猜(預測),誤差慢慢變大;
有 ODOM 數據時,用它修正猜測(更新),誤差縮小。
讓 IMU 當 “實時報信員”,隨時喊 “現在往哪動、動多快”; 讓 ODOM 當 “定期校準員”,每隔一會兒喊 “實際位置在這”; 裁判根據兩者的靠譜程度,綜合出一個最準的結果。
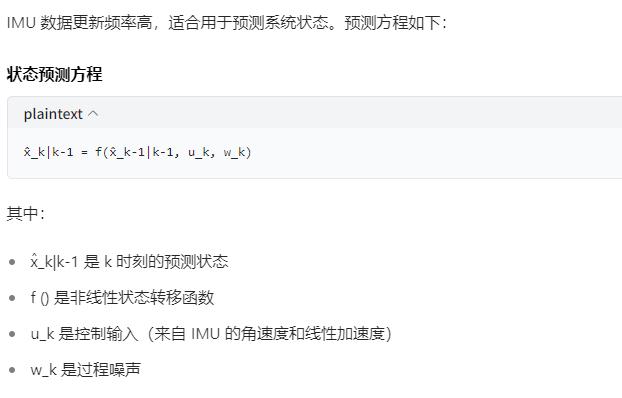
這個方程是擴展卡爾曼濾波器(EKF)的核心預測方程,確實比較抽象。我來一步步解釋,讓它變得更容易理解。
狀態預測方程的直觀理解
這個方程描述了如何根據上一時刻的狀態估計和當前的控制輸入,來預測當前時刻的系統狀態。
我們可以用一個生活中的例子來類比:
上一時刻的狀態:就像你現在知道自己的位置和速度
數學符號詳細解釋
讓我們拆解這個方程:

符號含義:
x?:帶帽子的 x 表示 "估計值"(不是真實值,因為有誤差)
k|k-1:豎線后面的數字表示 "基于哪個時刻的信息"
x?_k|k-1表示:基于 k-1 時刻的信息,對 k 時刻狀態的預測 x?_k-1|k-1表示:基于 k-1 時刻的信息,對 k-1 時刻狀態的估計(這是上一輪更新得到的結果) f():這是一個函數,表示狀態如何從一個時刻轉移到下一個時刻
u_k:控制輸入,例如 IMU 測量的加速度和角速度
w_k:過程噪聲,表示系統的不確定性(例如,你的動作可能不完全按照計劃執行)
更具體的例子:移動機器人
假設我們有一個在平面上移動的機器人,它的狀態包括:
位置:x, y
朝向:θ(角度) 速度:v_x, v_y(x 和 y 方向的速度)
總結
狀態預測方程x?_k|k-1 = f(x?_k-1|k-1, u_k, w_k)的核心思想是:
基于上一時刻的狀態估計
加上控制輸入的影響 考慮系統的不確定性 預測當前時刻的狀態
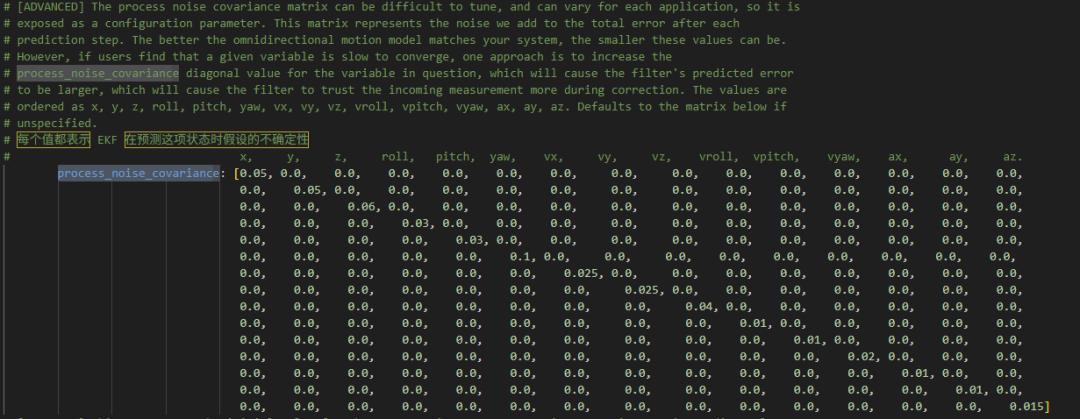
1. 矩陣結構與狀態對應
矩陣的行和列嚴格對應 EKF 狀態向量的順序,通常是:[x, y, z, roll, pitch, yaw, vx, vy, vz, vroll, vpitch, vyaw, ax, ay, az]
每個元素 process_noise_covariance[i][j] 的含義:
當 i=j(對角線元素):表示單個狀態量的預測噪聲強度(不確定性大小)。當 i≠j(非對角線元素):表示兩個狀態量之間的噪聲相關性(通常設為 0,假設各狀態噪聲獨立)。
2. 逐行 / 列解讀(以你的配置為例)
下面結合常見機器人運動場景(如差速底盤、機械臂),解釋對角線元素(非對角線多為 0,代表噪聲獨立)的物理意義:
| 位置 | |||
| 姿態(角) | |||
| 線速度 | |||
| 角速度 | |||
| 線加速度 | |||
3. 如何調參?核心邏輯
EKF 的本質是 **“信任模型預測” vs “信任傳感器觀測”** 的平衡,process_noise_covariance 控制對 “模型預測” 的信任度:
對角線值越小
:認為 “模型預測的狀態越準”,濾波會更依賴預測(適合模型精確的場景,比如高精度機械臂)。 對角線值越大
:認為 “模型預測的不確定性越高”,濾波會更依賴傳感器觀測(適合干擾多、模型粗糙的場景,比如地面機器人打滑)。
一句話總結
process_noise_covariance 是 EKF 的 “模型信任度旋鈕”—— 值越小,越相信模型預測;值越大,越依賴傳感器。調參時,先保持默認值跑場景,遇到 “收斂慢”(比如轉向后角度回不來)就增大對應維度的噪聲,遇到 “太敏感”(比如傳感器一飄就跟丟)就減小噪聲,反復迭代即可。



評論