基于小波變換微弱生命信號提取的研究
1 引言
生命信號由于受到人體等諸多因素的影響,具有信號弱、噪聲強、頻率范圍較低和隨機性強的特點,用傳統的傅里葉變換提取具有局限性。而具有多分辨分析特性的小波變換,可利用時頻平面上不同位置的不同分辨率,有效地從非平穩信號中提取瞬態信息,可有效地提取信號的波形。
2 Mallat算法
小波變換的多分辨分析MRA(Multi-Resolution-Analysis)特性,定義空間L2(R)中的一列子空間{Vj}j∈z,稱為L2(R)的一個多分辨分析(MRA),該序列若滿足下列條件:

Mallat根據多分辨分析提出小波變換分解和重構快速算法-Mallat算法。設({Vm;m∈Z};φ(t))是一個正交MRA,則存在{hk}∈ι2,使雙尺度方程:

方程(1)成立,并利用式(1)可得到尺度函數φ(x)構造函數:

ψ(x)的伸縮、平移構成L2(R)正交基,其中gk=(-1)h1-k。進一步,當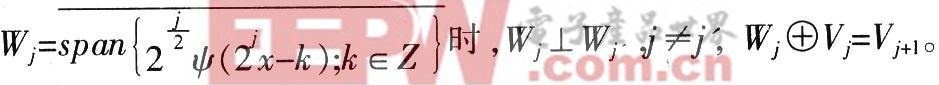
主要包含3個方面的內容:
(1)集合ψ0={φ(x-k);k∈Z}構成W0的標準正交基,因此![]() 構成Wj的標準正交基;
構成Wj的標準正交基;
(2)![]() 可以保證
可以保證![]() 從而保證Wj的基向量,并可表示L2(R)中的任意函數。
從而保證Wj的基向量,并可表示L2(R)中的任意函數。
(3)Wj⊥Wj',j≠j',保證在彼此正交的前提下當且僅當表示信息。
多分辨分析理論為信號局部分析提供相當直觀的框架,這一點在非平穩信號中的作用尤為重要,因為非平穩信號的頻率隨時間而變化,這種變化可分為慢變和快變兩部分,慢變部分對應于非平穩信號的低頻部分,代表信號的主要輪廓;而快變部分對應于信號的高頻信息,表示信號的細節,因此,Mallat算法的基本思想可以歸納如下:
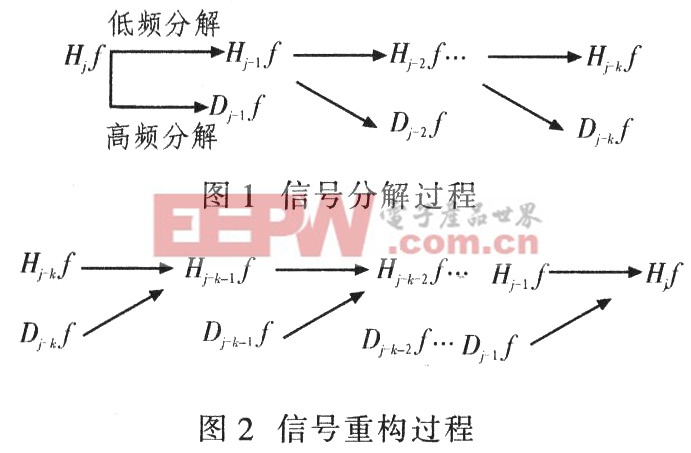
設Hjf為能量有限的信號f∈L2(R)在分辨率2j下的近似,則Hjf可以進一步分解為f在分辨率2j-1下的近似Hj-1f,以及位于分辨率2j-1與2j之間的細節Dj-1f之和,其分解和重構過程如圖1和圖2所示。






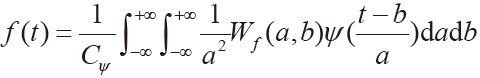
評論