S波段耦合腔行波管非線性注一波互作用方程組的數值

1 基本方程
1．1 激發方程
令第n次本征模式軸向電場為：

可得擾動電子注激勵的電場為：

式中：定義為n次諧波的耦合阻抗；

ψ(r⊥)為電子注橫向分布函數y）ds。所有本征模中只有個別模式與電子注同步，且除了電子流i（z）激發的同步波之外，還有輸入的“冷波”，即E0e-r0z，則具有外加激勵源E0e-r0z的同步場為：

式中：K0，г0，β0分別為該同步模式的耦合阻抗、傳播常數、相位常數。式(1)兩邊同時對z求導2次得到熟知的激發方程：

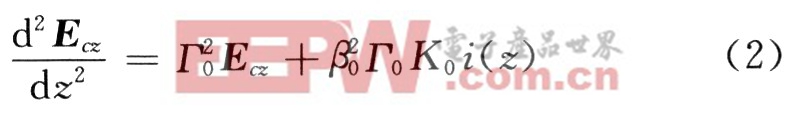
1．2 運動方程
相對論下電子的運動方程為：

能量守恒方程為：

式(4)代入式(3)可得一維電子運動方程：

又由：

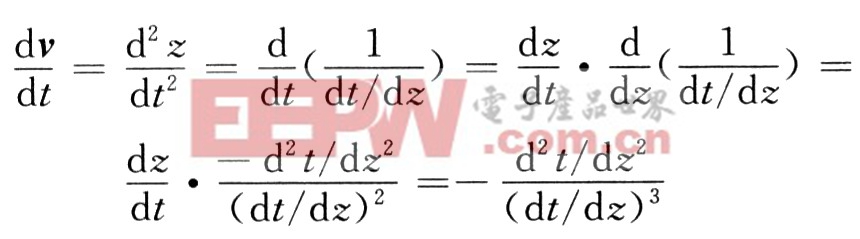
所以式(5)可寫為：

其中：Ez=Ecz(線路場)+Esz(空間電荷場)；y=(1一v2/c2)-1/2為相對論因子，c為真空中的光速，v為電子速度。
1．3 電子流復振幅方程
電子流是時間的非簡諧周期函數，含有高次諧波，用傅氏分析。

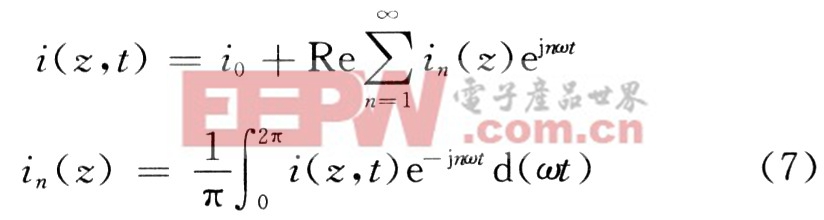
2 慢變系統中歸一化
上述是在實驗室坐標系下得到的迅變方程，為了處理問題的方便和計算結果普遍性強，通常將其歸一化到電子坐標系內，獲得慢變方程。
為了表述方便，先引入迅變坐標系的歸一化量：歸一化距離為ξ=ω/v0z=βez；歸一化時間為φ=ωt=2πt=/T，歸一化場為f=|e|E/mvoω。則慢變系統中的歸一化：歸一化軸向距離為θ=Cξ=Cβez；歸一化相位φe=ψ-ξ；歸一化場幅值為Fcn(θ)=(eE／C2mvoω)ejnθ；歸一化電流幅值為

式(8)～(10)組成了行波管大信號注一波互作用基本工作方程組。其中Cn3=I0Kcn/4V0為n次諧波增益參量，bn=(V0一Vpn)／C1Vpn非同步參量，dn=aon／βeCn為衰減常數，rn=bn-idn。

3 空間電荷場的計算
由文獻可知z0處圓盤在z處圓盤平面上各點產生的平均空間電荷場為：

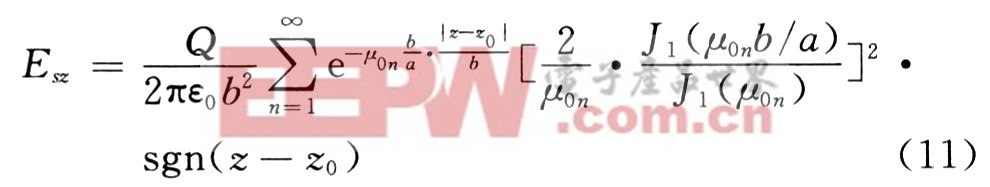
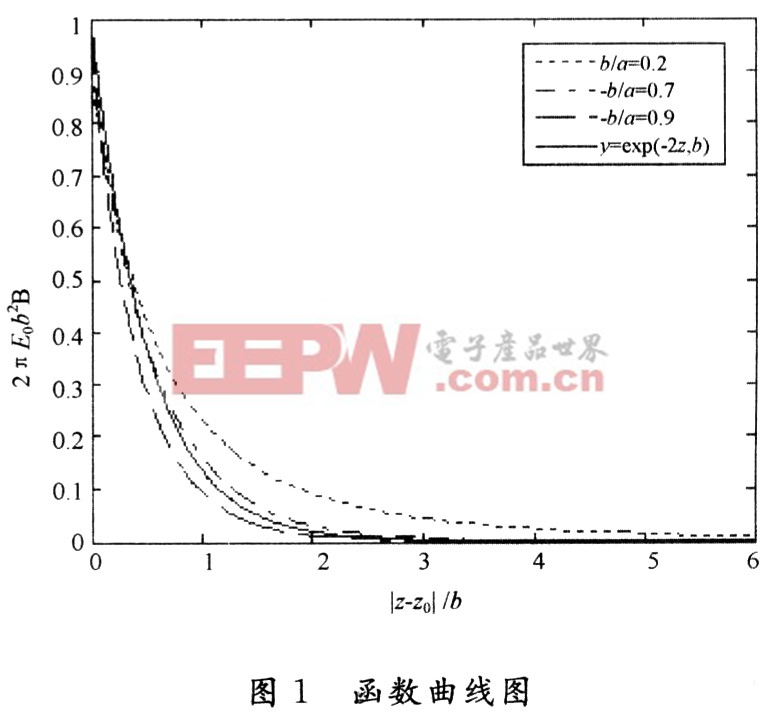
其中：Q為圓盤所帶電量；6為電子注半徑；a為漂移管半徑，如圖1所示，μ0n為零階Bessel函數的第n個根。由此可知場是關于z的函數，可以表示為：

其中：B(| z―z0|)是以| z―z0|為變量的函數，由式(11)可以做出如圖1所示曲線。