S波段耦合腔行波管非線性注一波互作用方程組的數值解

1 基本方程
1．1 激發(fā)方程
令第n次本征模式軸向電場為：

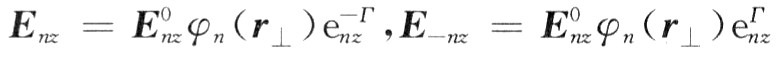
可得擾動電子注激勵的電場為：

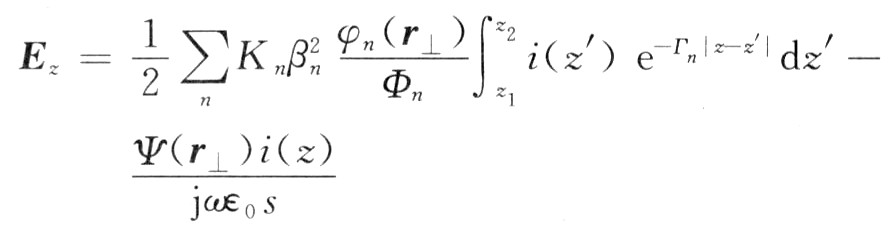
式中：定義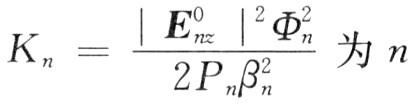為n次諧波的耦合阻抗；

ψ(r⊥)為電子注橫向分布函數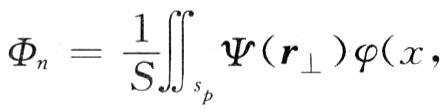y）ds。所有本征模中只有個別模式與電子注同步，且除了電子流i（z）激發(fā)的同步波之外，還有輸入的“冷波”，即E0e-r0z，則具有外加激勵源E0e-r0z的同步場為：

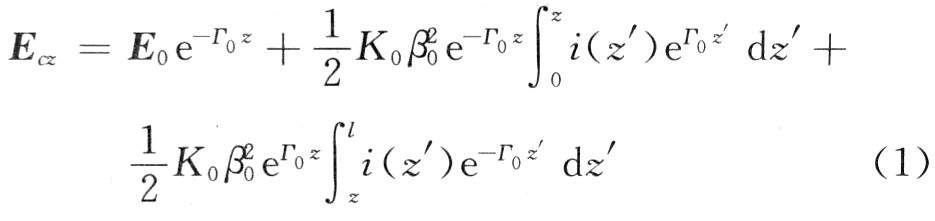
式中：K0，г0，β0分別為該同步模式的耦合阻抗、傳播常數、相位常數。式(1)兩邊同時對z求導2次得到熟知的激發(fā)方程：

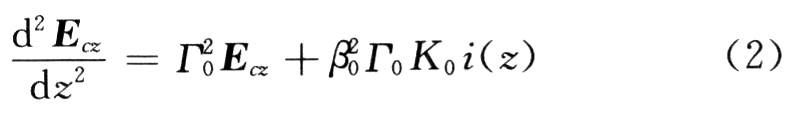
1．2 運動方程
相對論下電子的運動方程為：

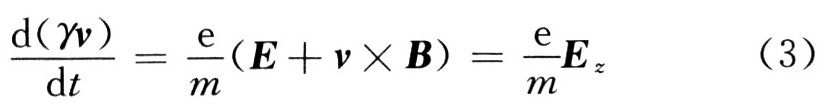
能量守恒方程為：

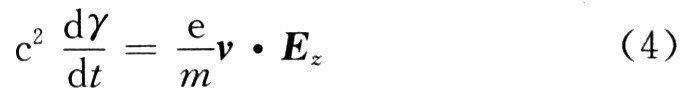
式(4)代入式(3)可得一維電子運動方程：

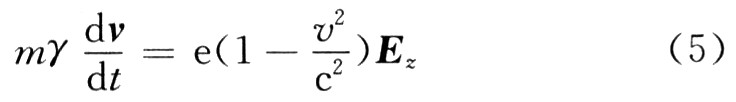
又由：

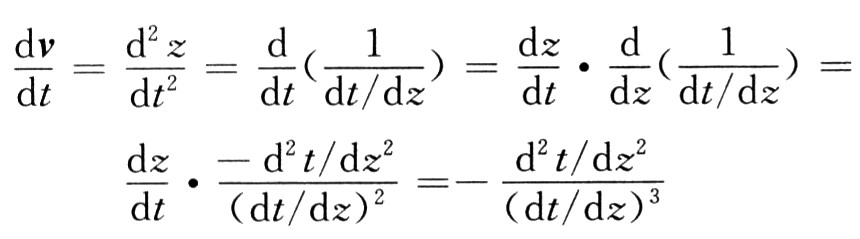
所以式(5)可寫為：

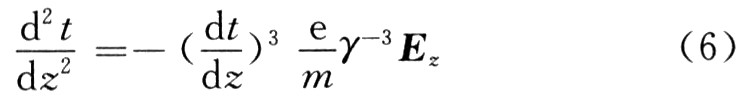
其中：Ez=Ecz(線路場)+Esz(空間電荷場)；y=(1一v2/c2)-1/2為相對論因子，c為真空中的光速，v為電子速度。
1．3 電子流復振幅方程
電子流是時間的非簡諧周期函數，含有高次諧波，用傅氏分析。

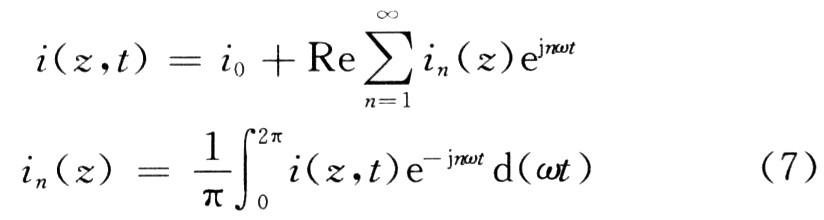
2 慢變系統(tǒng)中歸一化
上述是在實驗室坐標系下得到的迅變方程，為了處理問題的方便和計算結果普遍性強，通常將其歸一化到電子坐標系內，獲得慢變方程。
為了表述方便，先引入迅變坐標系的歸一化量：歸一化距離為ξ=ω/v0z=βez；歸一化時間為φ=ωt=2πt=/T，歸一化場為f=|e|E/mvoω。則慢變系統(tǒng)中的歸一化：歸一化軸向距離為θ=Cξ=Cβez；歸一化相位φe=ψ-ξ；歸一化場幅值為Fcn(θ)=(eE／C2mvoω)ejnθ；歸一化電流幅值為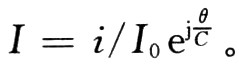

式(8)～(10)組成了行波管大信號注一波互作用基本工作方程組。其中Cn3=I0Kcn/4V0為n次諧波增益參量，bn=(V0一Vpn)／C1Vpn非同步參量，dn=aon／βeCn為衰減常數，rn=bn-idn。

3 空間電荷場的計算
由文獻可知z0處圓盤在z處圓盤平面上各點產生的平均空間電荷場為：

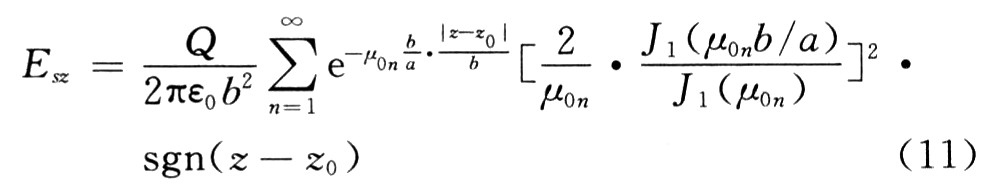
其中：Q為圓盤所帶電量；6為電子注半徑；a為漂移管半徑，如圖1所示，μ0n為零階Bessel函數的第n個根。由此可知場是關于z的函數，可以表示為：

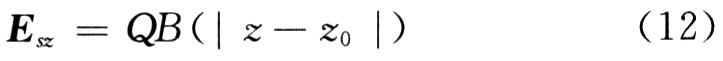
其中：B(| z―z0|)是以| z―z0|為變量的函數，由式(11)可以做出如圖1所示曲線。

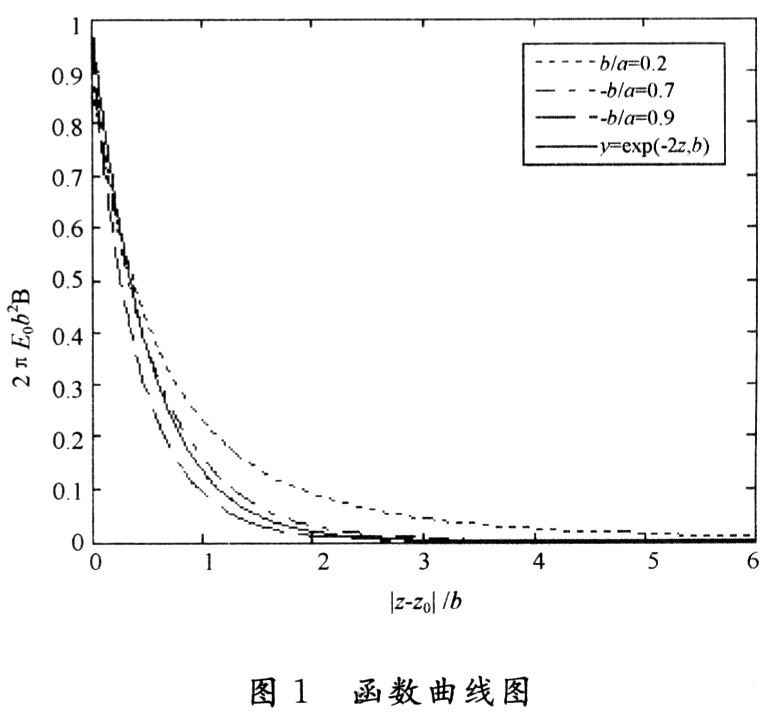
由圖1可知，如果用近似式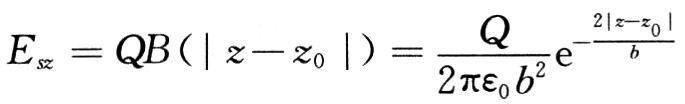代替式(11)，所引起的誤差很小，而計算式卻大大簡化了。采用該式時，所有圓盤產生的空間電

，
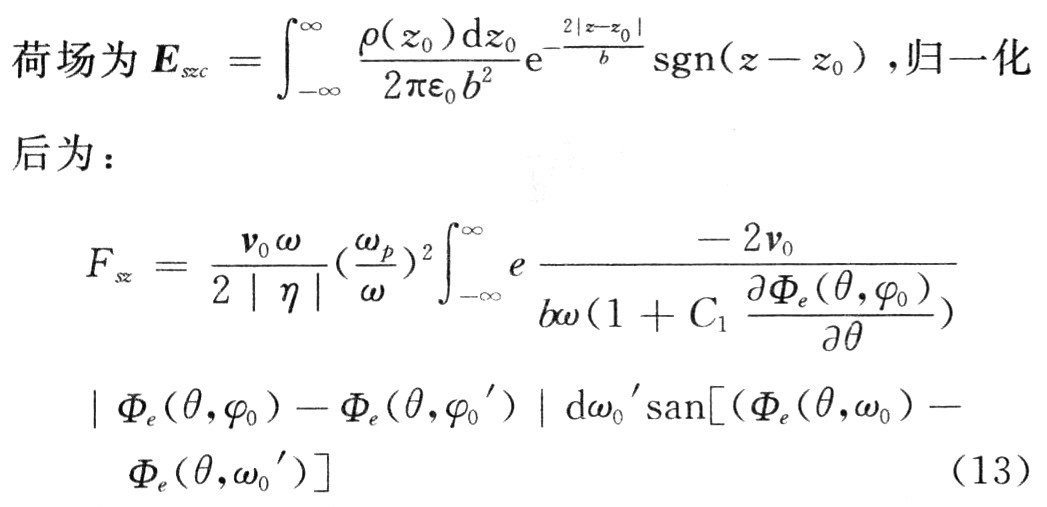其中：ωp為電子等離子體頻率；η為電子荷質比；v0為電子注初速度。仿真中用式(13)代替式(9)中的Fsz。

4 休斯結構耦合腔
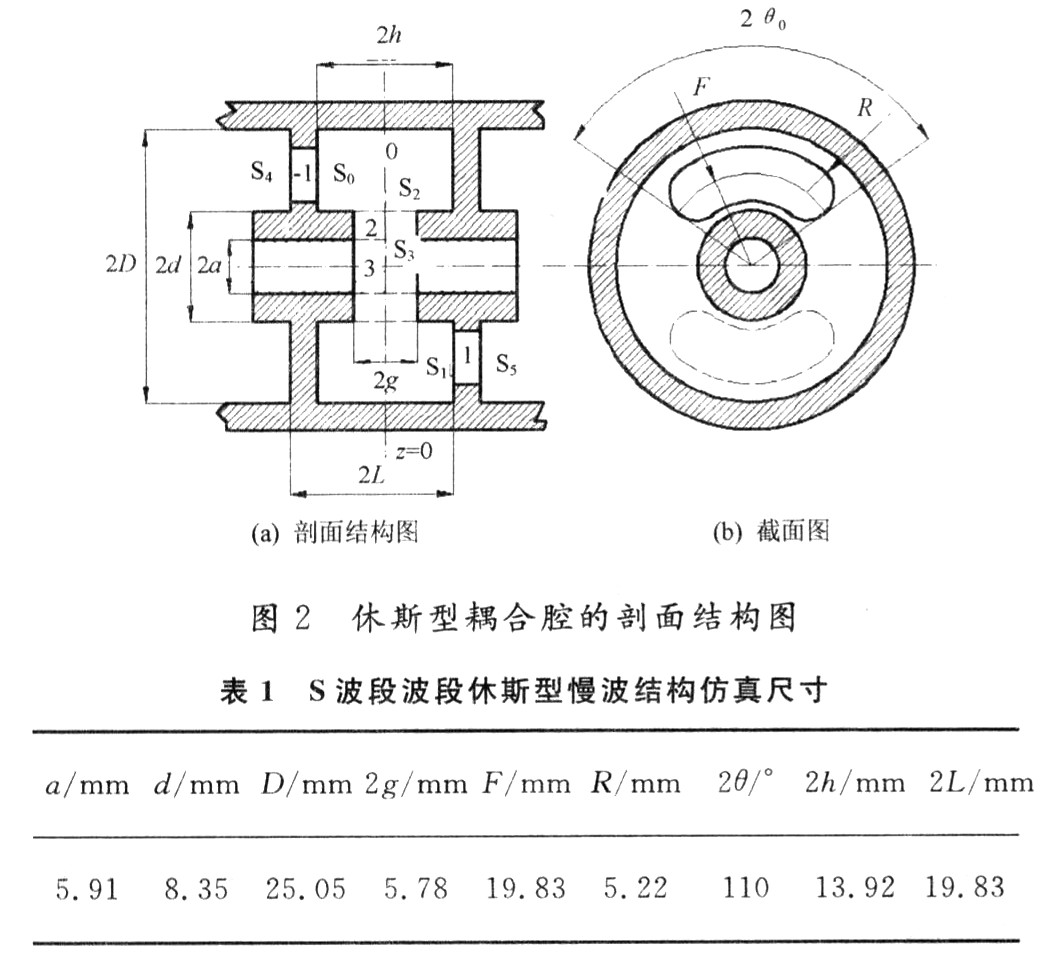
休斯型耦合腔的剖面結構為圖2(a)所示，圖2(b)為其截面圖，表1為設計s波段耦合腔行波管的結構參數。

5 仿真結果及討論
在上述尺寸下，對2．87～3．35 GHz頻率范圍內的休斯結構耦合腔行波管進行了數值分析，仿真中電子注的注電壓U。一21 kV，注電流L一1 A，波的輸入功率Pin=300 w。采用四階龍格一庫塔法求解互作用方程組式(8)～(10)，其結果如圖3～圖6所示。

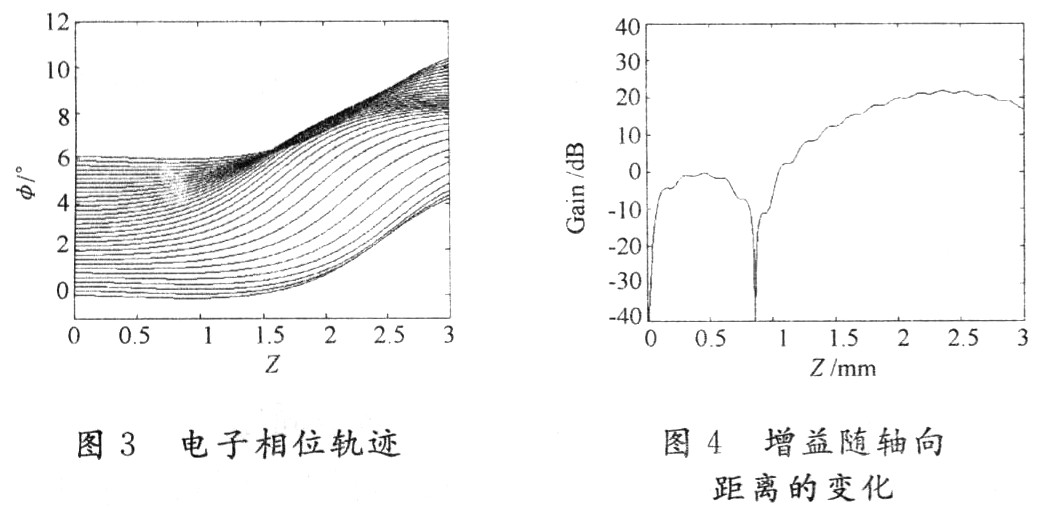
圖3給出了在中心頻率f=3．100 7 GHz時電子的相位軌跡。由圖可知，電子在歸一化軸向距離Z=2．4附近獲得了較好的群聚，此即為最佳互作用距離。由圖4可以看出該頻率的波在此處獲得最大增益，此后電子注離開最佳互作用區(qū)，效率降低，增益下降。

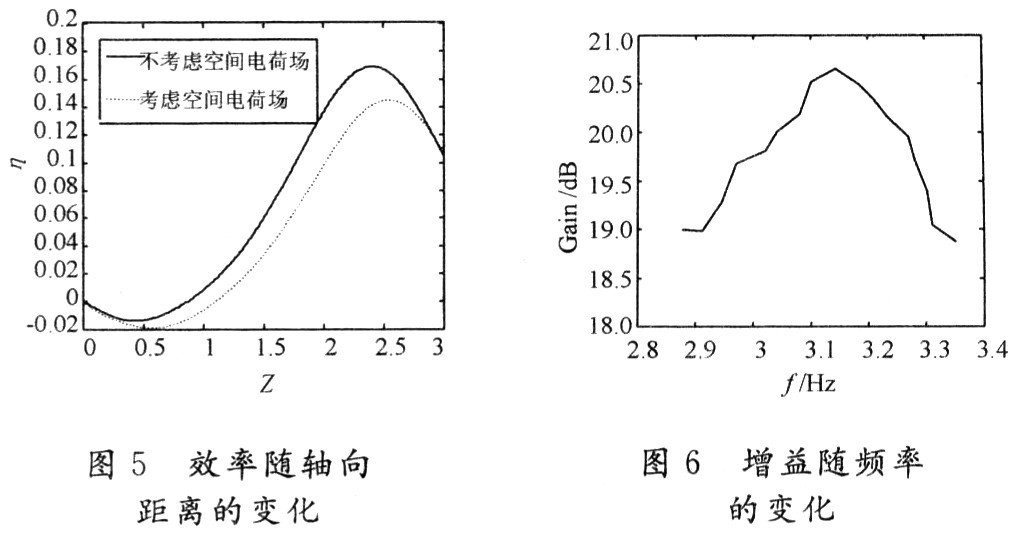
圖5給出了中心頻率時電子注效率隨軸向距離的變化曲線。圖中實線為不考慮空間電荷力的情況，虛線為考慮空間電荷力的情況。由圖可知，空間電荷力的作用使得飽和位置推后，增益下降，即空間電荷力起發(fā)散作用。圖中效率剛開始時為負值，是因為電子剛進入互作用區(qū)時要得到部分能量，表現電子效率為負值。
圖6給出考慮空間電荷場時，2．87～3．35 GHz內各頻點的微波增益。由圖可知，在給定電子注注電壓，注電流，和波的輸入功率等參量的情況下，頻帶內微波增益均大于18．5 dB。

6 結 語
對S波段休斯結構耦合腔行波管非線性注一波互作用工作方程組進行了數值求解，求出考慮和不考慮空間電荷場時中心頻率．廠一3．100 7 GHz處的效率，說明空間電荷場對互作用起散焦作用，與文獻中結論很吻合。求出工作在2．87～3．35 GHz頻率范圍內耦合腔行波瞬時帶寬。仿真中所用管子已制作完成，實驗數據對后期管子的熱測試有很好的指導意義。