指紋識(shí)別中的圖像處理研究------指紋圖像的特性分析 （一）

　　2指紋圖像的特性分析

　　一副指紋數(shù)字圖像是一個(gè)二維陣列，其陣列的元素值稱(chēng)為灰度值或者亮度值，在指紋圖像還沒(méi)有被量化成數(shù)字圖像之前，它是一個(gè)連續(xù)亮度函數(shù)的集合，指紋的特征信息就包含在這些亮度值中，在現(xiàn)有的指紋取像器件中，大部分是將指紋圖像量化成256個(gè)不同灰度級(jí)，也有32個(gè)灰度級(jí)的，對(duì)于確定身份的指紋識(shí)別技術(shù)而言，256個(gè)灰度級(jí)是應(yīng)用最廣泛的，本論文所指的指紋圖像如無(wú)特殊說(shuō)明均指256個(gè)灰度級(jí)的指紋圖像。圖2.1所示的是一個(gè)256灰度級(jí)的數(shù)字指紋圖像。

　　2.1數(shù)字圖像的幾何特性

　　對(duì)一幅數(shù)字圖像，如果要對(duì)其中包含目標(biāo)物體進(jìn)行識(shí)別和定位，經(jīng)常使用圖像區(qū)域的一些簡(jiǎn)單的特性，如大小、位置、方向，如果目標(biāo)物體的尺寸和形狀完全不同，則可以利用尺度和形狀特性來(lái)識(shí)別目標(biāo)物體。下面分別對(duì)數(shù)字圖像的大小、位置、方向進(jìn)行說(shuō)明。

　  2.1.1尺寸和位置

　　對(duì)于一幅m×n二值圖像B[i，j]，其目標(biāo)區(qū)域的面積A(或零階矩)由公式(2.1)給出，目標(biāo)區(qū)域的位置，用區(qū)域中心位置(x，y)表示來(lái)，目標(biāo)區(qū)域中心(x，y)可以用公式(2.2)來(lái)表示，將公式(2.2)進(jìn)一步化簡(jiǎn)可得到區(qū)域中心的計(jì)算公式(2.3)。

　　其中x和y是目標(biāo)區(qū)域中心在圖像中的行數(shù)和列數(shù)

　　由上式可以看出，區(qū)域中心是通過(guò)對(duì)圖像進(jìn)行全局運(yùn)算得到的一個(gè)點(diǎn)，因此它對(duì)圖像中的噪聲相對(duì)來(lái)說(shuō)不敏感。

　　2.1.2 方向

　　計(jì)算目標(biāo)物體的方向比計(jì)算它的位置要復(fù)雜，某些形狀(如圓)的方向不是唯一的，為了定義唯一的方向，一般假定物體是長(zhǎng)形的，其長(zhǎng)軸方向被定義為物體的方向。通常地，二維平面上與最小慣量軸同方向的最小二階矩軸被定義為長(zhǎng)軸。圖像中物體的二階矩軸是指這樣的一條直線，物體上的全部點(diǎn)到該直線的距離平方和最小，以二值圖像B[i,j]為例，圖像上目標(biāo)區(qū)域到最小二階矩軸的距離平方和χ2可用公式(2.4)表示。其中rij是目標(biāo)區(qū)域點(diǎn)[i,j]到直線的距離。在直線的點(diǎn)斜式表示中，當(dāng)直線處于近似垂直時(shí)，斜率的數(shù)值趨于無(wú)窮大，為了避免直線處于近似垂直時(shí)的這種數(shù)值病態(tài)問(wèn)題，把直線表示成極坐標(biāo)的形式，如公式(2.5)

　　所示如圖2.2所示

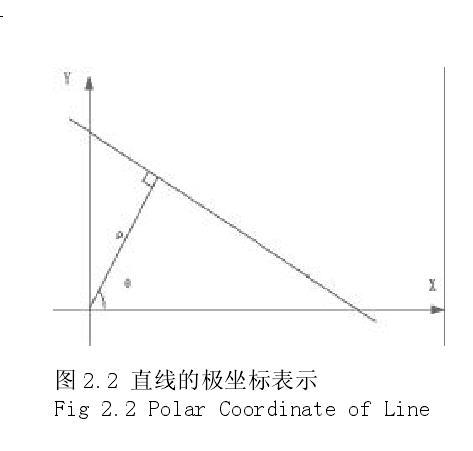
　　θ是直線的法線與x軸的夾角，ρ是直線到原點(diǎn)的距離，把圖像中的點(diǎn)[i ，j]坐標(biāo)帶入直線的極坐標(biāo)方程即可得出距離r，如公式(2.6)所示

　　將式(2.6)帶入式(2.4)可得式(2.7)

　　為了求得χ2最小時(shí)的常數(shù)ρ、θ值，可先對(duì)公式(2.7)求導(dǎo)數(shù)，令χ2對(duì)ρ的導(dǎo)數(shù)等于零，則可以得到公式(2.8)

　　化簡(jiǎn)公式(2.8)

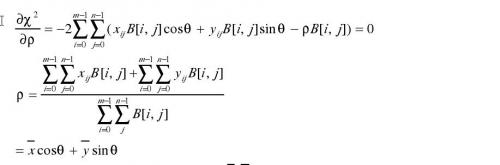
　　上式說(shuō)明回歸直線通過(guò)物體中心( x ，y)。將ρ的值帶入式(2.7)并且化簡(jiǎn)如

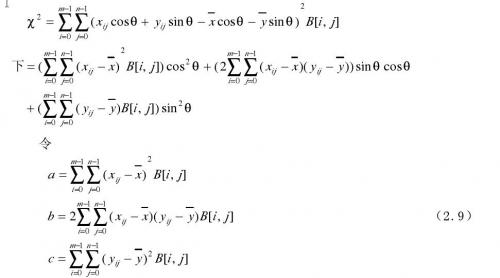
　　則

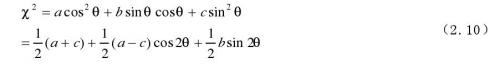
　　對(duì)式(2.10)中χ2微分，并且使微分結(jié)果為0，則得到式2.11

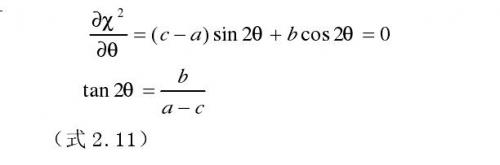
　　因此慣性軸的方向還可以用下面的公式給出

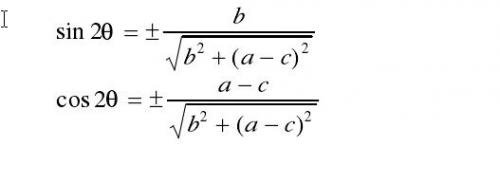
　　由式2.12可以確定4個(gè)θ值，其中當(dāng)θ取上述值時(shí)，χ2的取值可能是最小值，也可能是最大值，當(dāng)χ2取最小值時(shí)的θ值即為慣性軸的法線方向與x軸的夾角，這時(shí)方向軸可以唯一的確定。如果式2.12中b = 0， a=c，那么方向軸的方向就不是唯一的，因此方向軸就不能夠確定，或者說(shuō)該目標(biāo)區(qū)域沒(méi)有主方向。