非對稱密鑰RSA加密算法及其密鑰產生
一、 RSA算法是第一個能同時用于加密和數字簽名的算法,也易于理解和操作。 RSA是被研究得最廣泛的公鑰算法,從提出到現在已近二十年,經歷了各種攻擊的考驗,逐漸為人們接受,普遍認為是目前最優秀的公鑰方案之一。RSA的安全性依賴于大數的因子分解,但并沒有從理論上證明破譯RSA的難度與大數分解難度等價。即RSA的重大缺陷是無法從理論上把握它的保密性能如何,而且密碼學界多數人士傾向于因子分解不是NPC問題。RSA的缺點主要有:A)產生密鑰很麻煩,受到素數產生技術的限制,因而難以做到一次一密。B)分組長度太大,為保證安全性,n 至少也要 600 bits以上,使運算代價很高,尤其是速度較慢,較對稱密碼算法慢幾個數量級;且隨著大數分解技術的發展,這個長度還在增加,不利于數據格式的標準化。目前,SET(Secure Electronic Transaction)協議中要求CA采用2048比特長的密鑰,其他實體使用1024比特的密鑰。
其中公鑰e和私鑰d的求解過程分兩步:
主站蜘蛛池模板:
永平县|
新密市|
博客|
大城县|
高淳县|
高碑店市|
元谋县|
简阳市|
湖南省|
万全县|
武定县|
大庆市|
苍溪县|
左权县|
兴国县|
扶余县|
怀仁县|
镇雄县|
河池市|
容城县|
称多县|
祁东县|
嘉义市|
永新县|
炉霍县|
东山县|
南平市|
兴国县|
苗栗市|
红原县|
来宾市|
六安市|
巩义市|
平塘县|
三明市|
互助|
项城市|
兴和县|
平武县|
工布江达县|
新营市|
(1):隨機選取兩個100位(指十進制)以上的素數p和q;
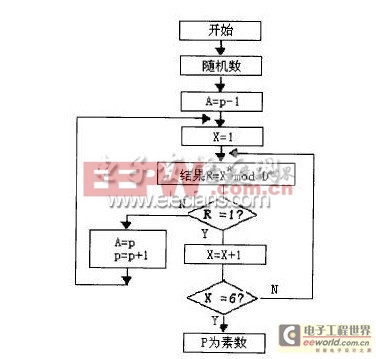
產生素數的方法:根據修改的歐拉定理,如p為素數,則對于X的所有整數值,應滿足:pow(X,(p一1))=1modP。
這是一個必要條件而非充分條件,不過,如果有5個以上的X值能滿足上述條件,則P可基本斷定為素數。圖1是產生素數的流程圖,該流程圖表示,如果X從1一5之間變化時,均能滿足上述條件,則P為素數,否則將P十1,重復計算,直到獲得素數為止。由此求得p和q,其乘積即為n。



評論