異步計數器

概述
一、計數器：用以統計輸入計數脈沖CP個數的電路。
計數器的“模”（用M表示）：
二、 計數器的分類
1．按計數進制分
2．按計數增減分
3．按計數器中觸發器翻轉是否同步分
7.3.1 異步計數器
一、異步二進制計數器

1．異步二進制加法計數
設計思想
JK觸發器組成4位異步二進制加法計數器
邏輯電路、工作原理、狀態轉換順序表、工作波形
D觸發器組成的4位異步二進制加法計數器（學生課后分析）
2．異步二進制減法計數器
設計思想
JK觸發器組成4位異步二進制減法計數器
邏輯電路、工作原理、狀態轉換順序表、工作波形

現代教學方法與手段：用DLCCAI或EWB演示異步二進制計數器的邏輯功能。

二、異步十進制加法計數器
4個JK觸發器組成的8421BCD碼異步十進制計數器
1．計數狀態順序表
2．邏輯電路圖
3．工作原理
4．工作波形

現代教學方法與手段：用DLCCAI或EWB演示異步十進制計數器的邏輯功能。

課堂討論：若考慮延遲時間，異步計數器的狀態從1111→0000的過程？
發現異步計數器的缺點，從而帶出同步計數器來。
7.3 計數器
概述
一、計數器：用以統計輸入計數脈沖CP個數的電路。
計數器的“模”（用M表示）：計數器累計輸入脈沖的最大數目。也為電路的有效狀態數。
如M＝6計數器，又稱六進制計數器。
二、 計數器的分類

1．按計數進制分

二進制計數器：按二進制數運算規律進行計數的電路稱作二進制計數器。
十進制計數器：按十進制數運算規律進行計數的電路稱作十進制計數器。
任意進制計數器：二進制計數器和十進制計數器之外的其它進制計數器統稱為任意進制計數器。如五進制計數器、六十進制計數器等。

2．按計數增減分

加法計數器：隨著計數脈沖的輸入作遞增計數的電路稱作加法計數器。
減法計數器：隨著計數脈沖的輸入作遞減計數的電路稱作減法計數器。
加/減計數器：在加/減控制信號作用下，可遞增計數，也可遞減計數的電路，稱作加/減計數器，又稱可逆計數器。
也有特殊情況，不作加/減，其狀態可在外觸發控制下循環進行特殊跳轉，狀態轉換圖中構成封閉的計數環。

3．按計數器中觸發器翻轉是否同步分

異步計數器：計數脈沖只加到部分觸發器的時鐘脈沖輸入端上，而其它觸發器的觸發信號則由電路內部提供，應翻轉的觸發器狀態更新有先有后的計數器，稱作異步計數器。
同步計數器：計數脈沖同時加到所有觸發器的時鐘信號輸入端，使應翻轉的觸發器同時翻轉的計數器，稱作同步計數器。顯然，它的計數速度要比異步計數器快得多。

7.3.1 異步計數器

一、異步二進制計數器
1．異步二進制加法計數
根據學生的程度，有時也可以從設計的角度，討論異步二進制加法計數器的設計思想。
復習（提問）：1 怎樣由JK F/F、D F/F實現T′F/F？
2 二進制加法的進位規則？

[必須滿足二進制加法原則：逢二進一（1+1=10，即Q由1加1→0時有進位）；
各觸發器應滿足兩個條件：
每當CP有效觸發沿到來時，觸發器翻轉一次，即用T′觸發器。
控制觸發器的CP端，只有當低位觸發器Q由1→0（下降沿）時，應向高位CP端輸出一個進位信號（有效觸發沿），高位觸發器翻轉，計數加1。]

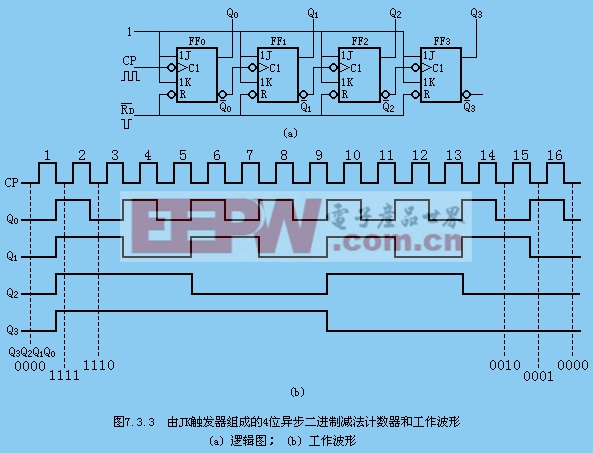
由JK觸發器組成4位異步二進制加法計數器
① 邏輯電路
JK觸發器都接成T′觸發器，下降沿觸發。

② 工作原理
異步置0端上加負脈沖，各觸發器都為0狀態，即Q3Q2Q1Q0＝0000狀態。在計數過程中，為高電平。
只要低位觸發器由1狀態翻到0狀態，相鄰高位觸發器接收到有效CP觸發沿，
T′的狀態便翻轉。

③ 狀態轉換順序表7.3.1所示。
電路為十六進制計數器。
④ 工作波形（又稱時序圖或時序波形）

輸入的計數脈沖每經一級觸發器，其周期增加一倍，即頻率降低一半。
一位二進制計數器就是一個2分頻器，
16進制計數器即是一個16分頻器。

表7.3.1 四位二進制加法計數器 狀態轉換順序表

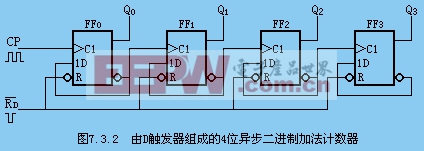
圖7.3.2所示為由D觸發器組成的4位異步二進制加法計數器的邏輯圖。
由于D觸發器用輸入脈沖的上升沿觸發，因此，每個觸發器的進位信號由 端輸出。
其工作原理類似，讓學生課后自行分析。

2．異步二進制減法計數器
根據學生的程度，有時也可以從設計的角度，討論異步二進制減法計數器的設計思想。
[二進制數的減法運算規則：1－1＝0，0—1不夠，向相鄰高位借位，10－1＝1；
各觸發器應滿足兩個條件：
每當CP有效觸發沿到來時，觸發器翻轉一次，即用T′觸發器。
控制觸發器的CP端，只有當低位觸發器Q由0→1（上升沿）時，應向高位CP端輸出一個借位信號（有效觸發沿），高位觸發器翻轉，計數減1。]

由JK觸發器組成的4位二進制減法計數器
① 邏輯圖。
FF3～FF0都為T′觸發器，下降沿觸發。
低位觸發器由0→ 1（上升沿）時，應向高位CP端輸出一個借位信號（有效觸發沿），而觸發器為下降沿觸發，低位觸發器應從 端輸出借位信號。

② 工作原理

表7.3.2 四位二進制減法計數器計數狀態順序表

二、異步十進制加法計數器
學習要點：十進制計數器的邏輯功能，即計數狀態順序表、工作波形。具體電路不要求掌握其電路形式，了解其電路工作原理（較復雜）。
異步十進制加法計數器是在4位異步二進制加法計數器的基礎上經過適當修改獲得的。它跳過了1010～1111六個狀態，利用自然二進制數的前十個狀態0000～1001實現十進制計數。
4個JK觸發器組成的8421BCD碼異步十進制計數器
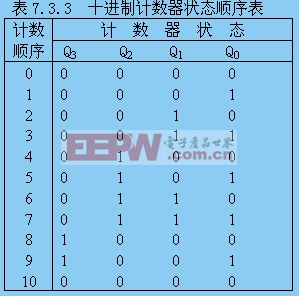
1．計數狀態順序表
表7.3.3 十進制計數器狀態順序表

2．邏輯電路圖

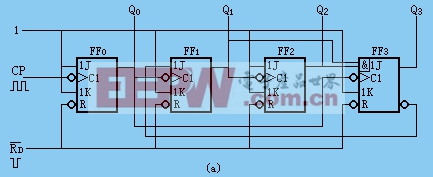
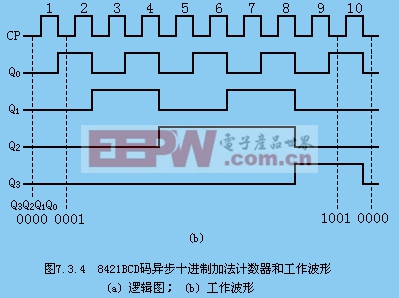
3．工作原理
FF0和FF2為T′觸發器。
設計數器從Q3Q2Q1Q0＝0000狀態開始計數。
這時J1==1，FF1也為T′觸發器。
因此，輸入前8個計數脈沖時，計數器按異步二進制加法計數規律計數。在輸入第7個計數脈沖時，計數器的狀態為Q3Q2Q1Q0＝0111。這時， J3＝Q2Q1＝1、 K3＝1。
輸入第8個計數脈沖時，FF0由1狀態翻到0狀態，Q0輸出的負躍變。一方面使FF3由0狀態翻到1狀態；與此同時，Q0輸出的負躍變也使FF1由1狀態翻到0狀態，FF2也隨之翻到0狀態。這時計數器的狀態為Q3Q2Q1Q0＝1000，=0使J1==0。因此，在Q3＝1時，FF1只能保持在0狀態，不可能再次翻轉。
輸入第9個計數脈沖時，計數器的狀態為Q3Q2Q1Q0＝1001。這時，J3＝0、K3＝1。
輸入第10個計數脈沖時，計數器從1001狀態返回到初始的0000狀態，電路從而跳過了1010～1111六個狀態，實現了十進制計數，同時Q3端輸出一個負躍變的進位信號。
4．工作波形。
課堂討論：若考慮延遲時間，異步計數器的狀態從1111→0000的過程？
可見，異步計數器存在過渡過程，若將狀態直接輸出到譯碼器，將會產生錯誤的譯碼，造成誤動作。這時，就要用下節課將要討論的同步計數器。

7.3.1 異步計數器
三、集成異步計數器CT74LS290
掌握查手冊使用MSI器件的方法。

㈠ 器件的邏輯功能
1．電路結構框圖
2．邏輯功能示意圖
3．功能表
4．邏輯功能說明
（1）異步置0功能。
（2）異步置9功能。
（3）計數功能。

㈡ 應用
1．實現10進制
附：用級聯（相當于串行進位）法實現N進制計數器的方法（異步）。
2．利用反饋歸零法獲得N（任意正整數）進制計數器
⑴ 計數器的置0功能
⑵ 利用反饋歸零法獲得N進制計數器

步驟：
① 寫出計數器狀態的二進制代碼。
② 寫出反饋歸零函數。這實際上是根據SN或SN-1寫置0端的邏輯表達式。
③ 畫連線圖。
［例7.3.1］ 試用CT74LS290構成六進制計數器。
將CT74LS290構成九進制計數器。

7.3.3 利用計數器的級聯獲得大容量N進制計數器
一、級聯法

例：實現100進制計數器

二、反饋歸零法

例：實現異步二十三進制計數器

7.3.1 異步計數器
三、集成異步計數器CT74LS290
掌握查手冊使用MSI器件的方法。
㈠ 器件的邏輯功能
1．電路結構框圖（未畫出置0和置9輸入端）：
二進制計數器 + 五進制計數器。
所以又稱為：集成異步二—五一十進制計數器
2．邏輯功能示意圖
說明：MSI器件畫邏輯功能示意圖的方法。
⑴ 先畫一個矩形框
⑵ 在矩形框中填入MSI器件的型號
⑶ 在矩形框的四周畫輸入、輸出引線，位置根據需要而定，原則是使構成的電路原理清析，簡單明了。一般CP信號加上“＞”符號，低電平有效時加小圓圈。
ROA和ROB：置0輸入端，都為高電平時有效置0（即0000）
S9A和S9B：置9輸入端，都為高電平時有效置9（即1001）

思考：若置0、置9同時有效，結果如何？置9。一般不允許出現。

4．邏輯功能說明

（1）異步置0功能。

計數脈沖由CP0輸入，從Q0輸出時，則構成一位二進制計數器
計數脈沖由CP1端輸入，輸出為Q3Q2Q1Q0時，則構成異步五進制計數器。

㈡ 應用
1．實現10進制

附：用級聯（相當于串行進位）法實現N進制計數器的方法（異步）。

課堂討論：級聯法實現更大容量計數器時，計數器的順序如何？
這樣構成的N進制計數器的計數狀態將保留M1進制計數器的特點。
8421BCD碼十進制計數器狀態表5421BCD碼十進制計數器狀態表

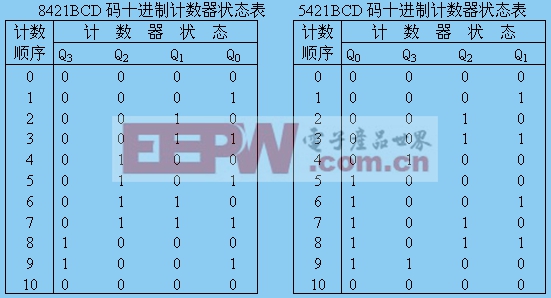
如將Q0和CP1相連，計數脈沖由CP0輸入，輸出為Q3Q2Q1Q0時，則構成8421BCD碼異步十進制計數器。2×5=10
復習（提問）：5421BCD碼？
如將Q3和CP0相連，計數脈沖由CP0端輸入，從高位到低位的輸出為Q0Q3Q2Q1時，則構成5421BCD碼異步十進制加法計數器。5×2=10

2．利用反饋歸零法獲得N（任意正整數）進制計數器

⑴ 計數器的置0功能
集成計數器的置0方式有異步和同步兩種。
①異步置0：與時鐘脈沖CP沒有任何關系，只要異步置0輸入端出現置0信號，計數器便立刻被置0。
② 同步置0：輸入端獲得置0信號后，只是為置0創造了條件，還需要再輸入一個計數脈沖CP，計數器才被置0。

⑵ 利用反饋歸零法獲得N進制計數器
用S0，S1，S2…，SN表示輸入0，1，2，…，N個計數脈沖CP時計數器的狀態。
N進制計數器的計數工作狀態應為N個：S0，S1，S2…，SN-1
對于異步置0：在輸入第N個計數脈沖CP后，通過控制電路，利用狀態SN產生一個有效置0信號，送給異步置0端，使計數器立刻置0，即實現了N進制計數。
對于同步置0：在輸入第N－1個計數脈沖CP時，利用狀態SN-1產生一個有效置0信號，送給同步置0端，等到輸入第N個計數脈沖CP時，計數器才被置0，回到初始的零狀態，從而實現N進制計數。

課堂討論：異步置0時狀態SN出現的時間有多久？

步驟：
① 寫出計數器狀態的二進制代碼。
下面以構成十二進制計數器為例進行說明。
當利用異步置0端獲得十二進制計數器時，SN＝S12＝1100；
當利用同步置0端獲得十二進制計數器時，SN-1＝S12-1＝S11＝1011。
② 寫出反饋歸零函數。
根據SN或SN-1寫置0端的邏輯表達式。

若用CT74LS290（異步置0）構成十二進制計數器，用SN ，

可令R0A= Q3，R0B＝Q2
③ 畫連線圖。主要根據反饋歸零函數畫連線圖。

［例7.3.1］ 試用CT74LS290構成六進制計數器。

解：（1）寫出S6的二進制代碼為
S6＝0110
（2）寫出反饋歸零函數。由于CT74LS290的異步置0信號為高電平1，因此，

（3）畫連線圖。
首先實現8421BCD碼的十進制計數器。
再將異步置0輸入端R0A和R0B分別接Q2、Q1，同時將R9A和R9B接0。
如圖7.3.6（a）所示。

［例7.3.2］：將CT74LS290構成九進制計數器，如圖7.3.6（b）所示。

圖7.3.6 用CT74LS290構成六進制計數器和九進制計數器
（a） 六進制計數器；（b）九進制計數器

7.3.3 利用計數器的級聯獲得大容量N進制計數器
一、級聯法

計數器的級聯是將多個集成計數器（如M1進制、M2進制）串接起來，以獲得計數容量更大的N（=M1×M2）進制計數器。
一般集成計數器都設有級聯用的輸入端和輸出端。
異步計數器實現的方法：低位的進位信號→高位的CP端

兩片接成十進制的CT74LS290級聯組成10×10=100進制異步加法計數器。

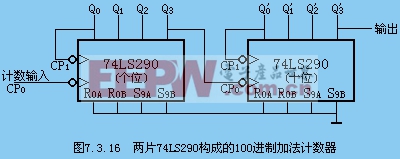
二、反饋歸零法

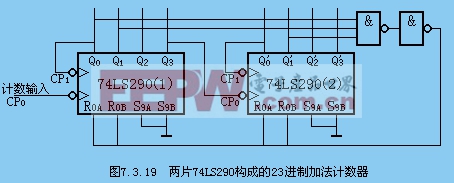
例：實現異步二十三進制計數器
首先由兩片CT74LS290構成的100進制計數器。
再利用反饋歸零法，S23的二進制代碼：0010 0011
當高位片CT74LS290（2）計到2、低位片計到3時，兩級與非門輸出高電平1，加到異步置0端，使計數器回到初始的0狀態，從而實現了二十三進制計數。