頻率響應法--極坐標圖
|
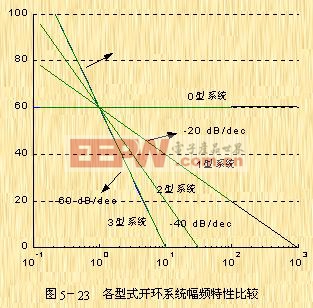 |
式(5-41)所示的是一簇斜率為![]() 的直線,且在
的直線,且在 ![]() 處,
處, ![]() ,如圖5-23所示。由式(5-41)求得,這些不同斜率的直線通過0dB-44)中的1和
,如圖5-23所示。由式(5-41)求得,這些不同斜率的直線通過0dB-44)中的1和 ![]() 項,則得
項,則得
![]()
上式表示![]() 的高頻漸近線為一斜率
的高頻漸近線為一斜率 ![]() 的直線。不難看出,兩條漸近線相交于
的直線。不難看出,兩條漸近線相交于 ![]() 。
。 ![]() 稱為振蕩環節的轉折頻率。基于實際的對數幅頻特性既與頻率
稱為振蕩環節的轉折頻率。基于實際的對數幅頻特性既與頻率 ![]() 和
和 ![]() 有關,又與阻尼比
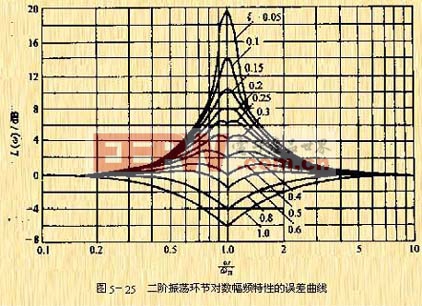
有關,又與阻尼比 ![]() 有關,因而這種環節的對數幅頻特性曲線一般不能用其漸近線近似表示,不然會引起較大的誤差。圖5-25所示。由圖可見,
有關,因而這種環節的對數幅頻特性曲線一般不能用其漸近線近似表示,不然會引起較大的誤差。圖5-25所示。由圖可見, ![]() 值越小,對數幅頻曲線的峰值就越大,它與漸近線之間的誤差也就越大。
值越小,對數幅頻曲線的峰值就越大,它與漸近線之間的誤差也就越大。
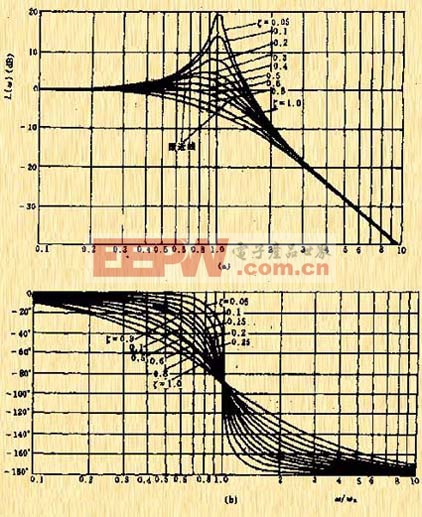 |
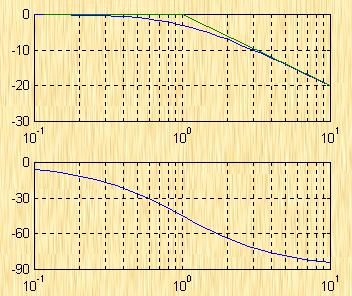
| 圖5-24 二階振蕩環節的對數幅頻特、漸近線和相角曲線 |
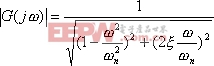
將式(5-43)的幅值表達式寫為
 |
|
令
|
 |
顯然,如在某一頻率時,![]() 有最小值,則
有最小值,則 ![]() 便有最大值。把式(5-46)改寫為
便有最大值。把式(5-46)改寫為
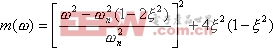 |
|
下面針對不同的![]() 值范圍,討論在什么條件下,式(5-44)會有峰值出現,這個峰值和相應的頻率應如何計算。
值范圍,討論在什么條件下,式(5-44)會有峰值出現,這個峰值和相應的頻率應如何計算。
(1)![]() 時
時
從式(5-47)中看出,當![]() 時,
時, ![]() 有最小值,即
有最小值,即 ![]() 有最大值,這個最大值稱為諧振峰值,用
有最大值,這個最大值稱為諧振峰值,用 ![]() 表示之。基于
表示之。基于 ![]() 值為
值為 ![]() ,由式(5-26所示。產生諧振峰值時的頻率叫諧振頻率,用
,由式(5-26所示。產生諧振峰值時的頻率叫諧振頻率,用 ![]() 表示,它的值為
表示,它的值為
由上式可見,當![]() 趨于零時,
趨于零時, ![]() 就趨向于
就趨向于 ![]() 。當
。當 ![]() 時,
時, ![]() 總小于有阻尼自然頻率
總小于有阻尼自然頻率 ![]() 。
。
(2)![]() 時
時
此時可將式(5-46)改寫為
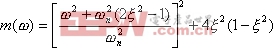 |
|
不難看出,由于![]() 隨著
隨著



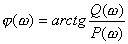

評論