十六進制數字

十六進制數字將二進制數每四位分為一組，從而能夠表示16種不同的二進制位組合。

二進制與十六進制都是基于不同基數的位值計數系統。二進制采用基數為2的系統，而十六進制采用基數為16的系統。用二進制表示十進制（基數為10）數字的主要缺點之一是：等效的二進制字符串（由1和0組成）可能非常冗長且容易混淆。

在處理大型數字系統時，經常會遇到由8位、16位甚至32位單獨數字組成的二進制數。這些長串數字在讀寫時極易出錯，尤其是在處理大量16位或32位二進制數時。

解決這一問題的常見方法是將二進制數按4位一組進行劃分。這種4位分組采用了另一種常用于計算機和數字系統的計數系統——十六進制數字。

十六進制數字串

“十六進制”（簡稱“Hex”）系統采用基數為16的計數方式，因其格式緊湊且比冗長的二進制串更易理解，成為表示長二進制值的常用選擇。

作為基數為16的系統，十六進制使用16個不同的數字符號，涵蓋從0到15的所有組合。換句話說，共有16種可能的數字符號。

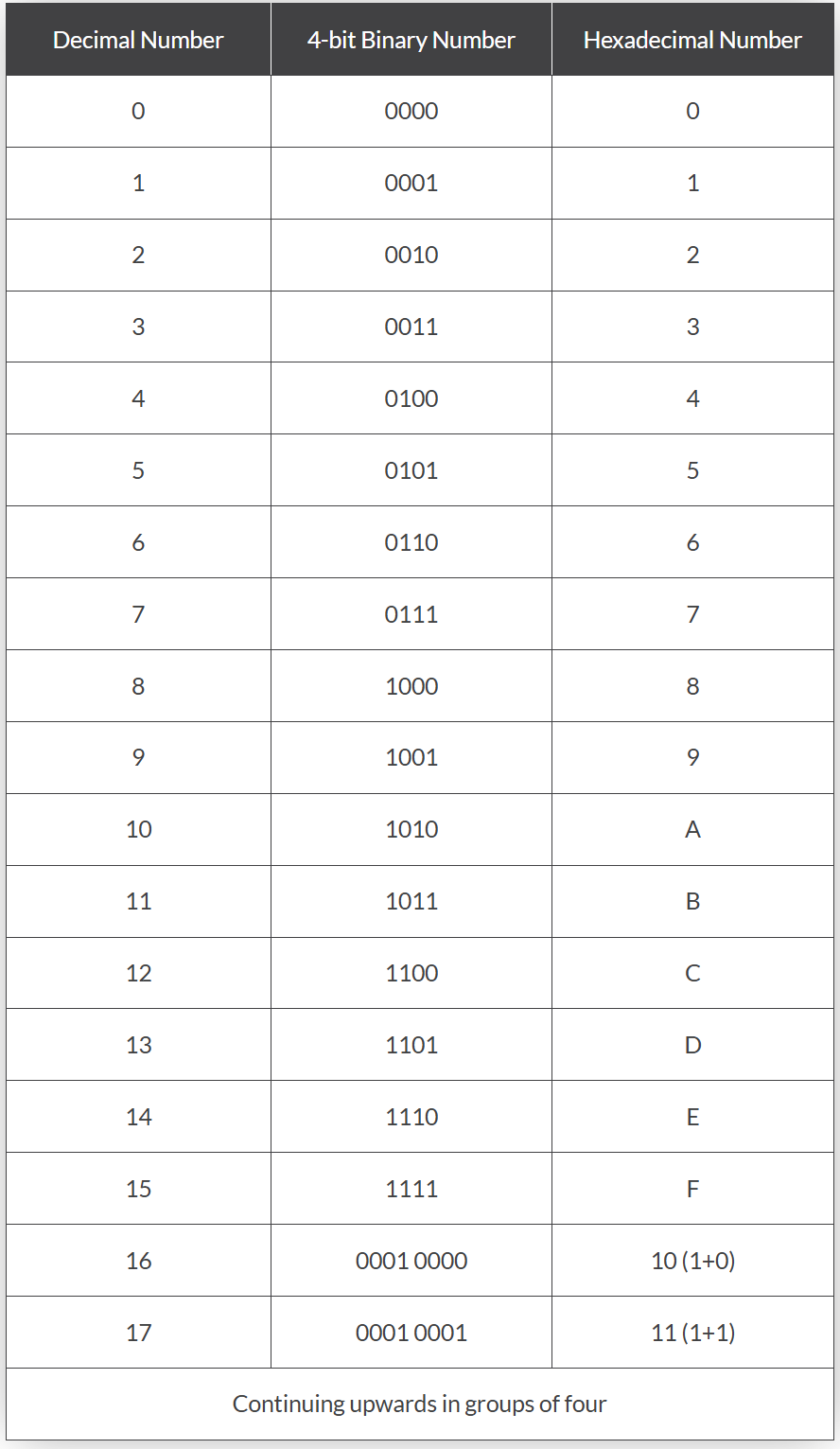
然而，這種表示方法存在一個潛在問題：十進制中的10、11、12、13、14和15通常需要兩個相鄰符號來表示。例如，十六進制中的“10”究竟表示十進制數字“十”，還是二進制數字“二”（1+0）？

為避免混淆，十六進制用大寫字母A、B、C、D、E和F分別代表十進制中的10、11、12、13、14和15。因此，十六進制系統使用數字0到9和字母A到F來表示對應的二進制或十進制數值，并從右側最低有效位開始排列。

二進制分組的優勢

如前所述，二進制串可能冗長難讀。但通過將其劃分為均勻的組別，可以大幅提升可讀性。例如：

1101  0101  1100  11112比連續排列的11010101110011112更易于理解。

日常使用的十進制系統會從右至左每三位分組（如千分位符），以便理解百萬或萬億等大數字。數字系統同樣適用這一邏輯。

十六進制的應用場景

十六進制比純二進制或十進制更復雜，主要用于處理計算機和內存地址定位。將二進制數劃分為4位一組后，每組的值范圍可從“0000”（0）到“1111”（8+4+2+1=15），共16種組合（注意“0”也是有效數字）。

在二進制教程中我們提到，4位數字稱為“半字節”（nibble）。由于十六進制數也需4位表示，一個十六進制數字可視為半字節或半個字節。因此，兩個十六進制數（00到FF）可構成一個完整字節。

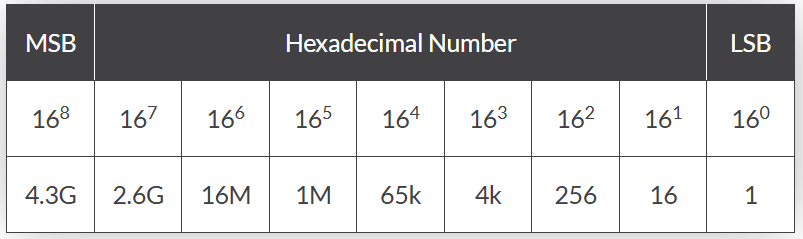
由于十進制中的16是2的四次方（2?），二進制與十六進制存在直接對應關系：一個十六進制位等于四個二進制位（此時基數q=16）。

轉換優勢

基于這種關系，四位二進制數可用單個十六進制位表示。這使得二進制與十六進制之間的轉換極為便捷，并能用更少位數表示大型二進制數。

數字0到9仍沿用十進制符號，而10到15用字母A到F表示。三者對應關系如下：

例如，將二進制數1101 0101 1100 11112轉換為十六進制后得到D5CF，遠比原始二進制串清晰。

核心特性

十六進制系統的主要特征包括：

-包含16個獨立計數符號（0到F）；

-每位權重為16的冪（從最低有效位開始）。

為區分十六進制與十進制數，通常在數值前添加前綴“#”（井號）或“$”（美元符號），如D5CF或$D5CF。

由于十六進制的基數為16（也代表系統使用的符號數量），可用下標16標識十六進制數。例如：D5CF??。

十六進制計數規則

當計數超過字母F時，需新增一組4位二進制。例如：

0…9,A…F,10…19,1A…1F,20,21…

注意：十六進制的“10”表示“1+0”（即十進制16），而非十進制的“十”。同理，“20”表示“2×16”。

用兩位十六進制數可計數至FF??（即十進制255）。若要繼續計數，需在左側添加第三位。例如：

-首位3位十六進制數為100??（十進制256）；

-最大3位數為FFF??（十進制4095）；

-最大4位數為FFFF??（十進制65,535），依此類推。

十六進制數字的表示方法

若需轉換的二進制位數為4、8、12或16位，將其轉換為十六進制數會非常簡單。但如果二進制位數不是4的倍數，我們可以在最高有效位（MSB）左側補零。

例如，11001011011001是一個14位二進制數，它超過3位十六進制數的表示范圍，但又不足4位十六進制數的完整組。解決方法是在最左側補零，直到形成完整的4位組或其倍數。

二進制數補零示例

這種補零方法適用于任意長度的二進制數。例如，若有一個9位二進制數需轉換為4位十六進制數（16位），則需在左側補7個零：

0000000111111111?=01FF??

十六進制數的優勢

十六進制數的主要優勢在于其緊湊性。基數為16的特性使得表示同一數值所需的位數通常少于二進制或十進制。此外，十六進制與二進制之間的轉換非常快捷。

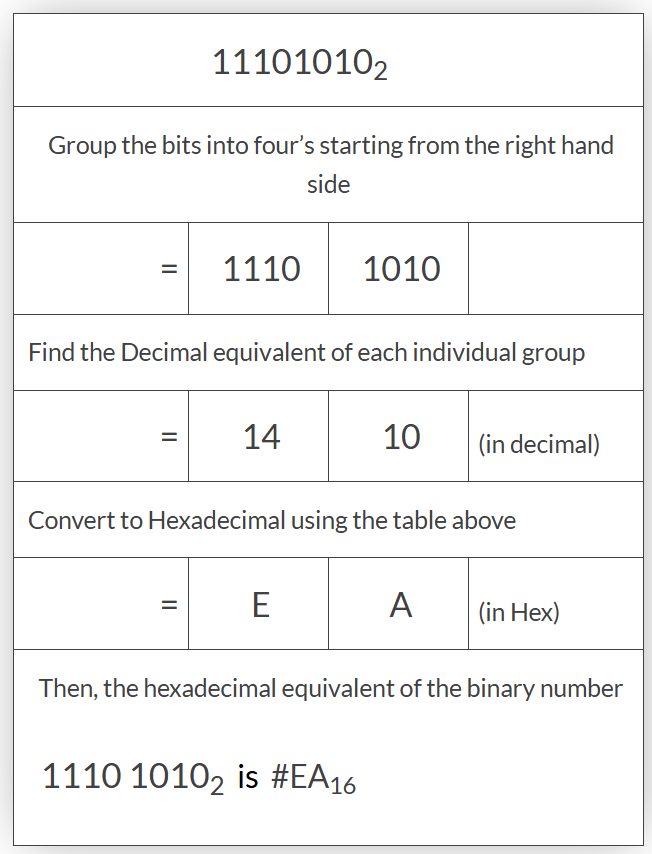
十六進制轉換示例1

將二進制數11101010?轉換為十六進制：

十六進制轉換示例2

將十六進制數3FA7??轉換為二進制和十進制：

十六進制系統總結

十六進制（Hex）系統通過將長二進制串壓縮為4位一組，顯著提升了數字的可讀性。其名稱“Hexadecimal”源于該系統使用的16個符號：0-9和A-F。

核心要點：

-二進制數需按4位分組，每組對應十六進制的0-F。

-通過補零可適配非4倍數的二進制長度。

-十六進制在計算機系統中廣泛用于簡化二進制表達。

在后續關于二進制邏輯的教程中，我們將探討如何將二進制串轉換為另一種數字系統——八進制數，反之亦然。