Transformer、RNN和SSM的相似性探究：揭示看似不相關(guān)的LLM架構(gòu)之間的聯(lián)系

通過探索看似不相關(guān)的大語言模型(LLM)架構(gòu)之間的潛在聯(lián)系，我們可能為促進(jìn)不同模型間的思想交流和提高整體效率開辟新的途徑。

盡管Mamba等線性循環(huán)神經(jīng)網(wǎng)絡(luò)(RNN)和狀態(tài)空間模型(SSM)近來備受關(guān)注，Transformer架構(gòu)仍然是LLM的主要支柱。這種格局可能即將發(fā)生變化：像Jamba、Samba和Griffin這樣的混合架構(gòu)展現(xiàn)出了巨大的潛力。這些模型在時間和內(nèi)存效率方面明顯優(yōu)于Transformer，同時在能力上與基于注意力的LLM相比并未顯著下降。

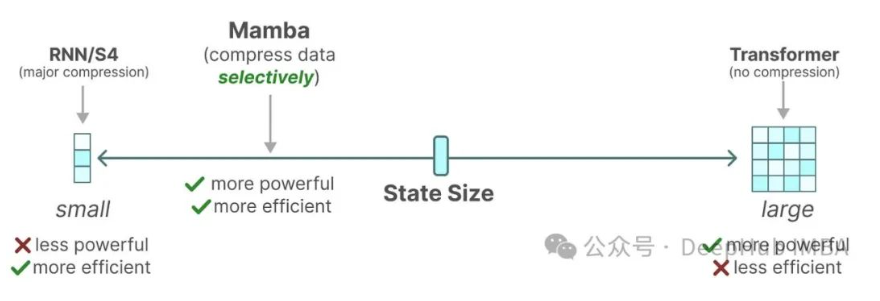
近期研究揭示了不同架構(gòu)選擇之間的深層聯(lián)系，包括Transformer、RNN、SSM和matrix mixers，這一發(fā)現(xiàn)具有重要意義，因為它為不同架構(gòu)間的思想遷移提供了可能。本文將深入探討Transformer、RNN和Mamba 2，通過詳細(xì)的代數(shù)分析來理解以下幾點:

● Transformer在某些情況下可以視為RNN(第2節(jié))

● 狀態(tài)空間模型可能隱藏在自注意力機制的掩碼中(第4節(jié))

● Mamba在特定條件下可以重寫為掩碼自注意力(第5節(jié))

這些聯(lián)系不僅有趣，還可能對未來的模型設(shè)計產(chǎn)生深遠(yuǎn)影響。

LLM中的掩碼自注意力機制

首先,讓我們回顧一下經(jīng)典的LLM自注意力層的結(jié)構(gòu)：

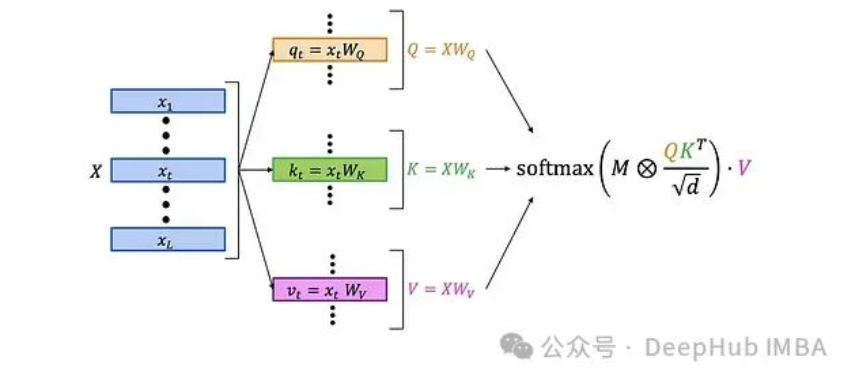
更詳細(xì)的結(jié)構(gòu)如下：

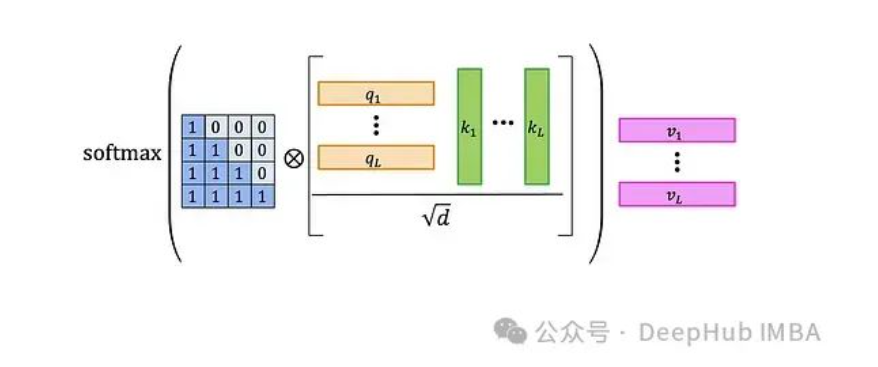
自注意力層的工作流程如下：

● 將查詢矩陣Q和鍵矩陣K相乘，得到一個L×L的矩陣，包含查詢和鍵的標(biāo)量積。

● 對結(jié)果矩陣進(jìn)行歸一化。

● 將歸一化后的矩陣與L×L的注意力掩碼進(jìn)行元素級乘法。圖中展示了默認(rèn)的因果掩碼——左側(cè)的0-1矩陣。這一步驟將較早查詢與較晚鍵的乘積置零，防止注意力機制"看到未來"。

● 對結(jié)果應(yīng)用softmax函數(shù)。

● 最后，將注意力權(quán)重矩陣A與值矩陣V相乘。輸出的第t行可表示為：

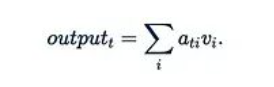
這意味著第i個值是通過"第t個查詢對第i個鍵的注意力權(quán)重"來加權(quán)的。

這種架構(gòu)中的多個設(shè)計選擇都可能被修改。接下來我們將探討一些可能的變體。

線性化注意力

注意力公式中的Softmax函數(shù)確保了值是以和為1的正系數(shù)混合的。這種設(shè)計保持了某些統(tǒng)計特性，但同時也帶來了限制。例如即使我們希望利用結(jié)合律，如(QK^T)V = Q(K^TV),也無法突破Softmax的限制。

為什么結(jié)合律如此重要？因為改變乘法順序可能顯著影響計算復(fù)雜度：

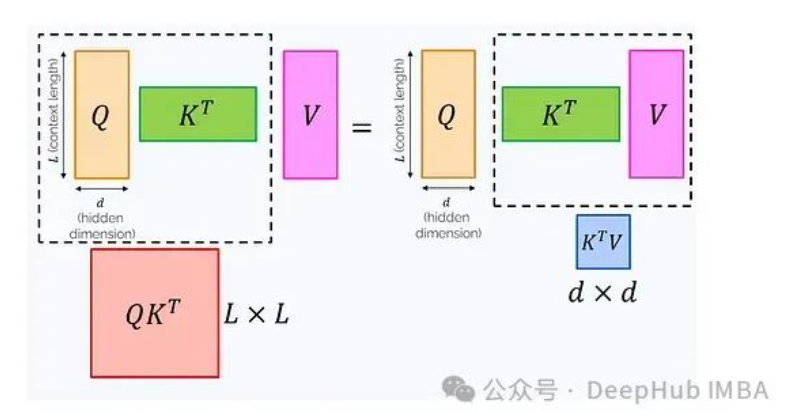
左側(cè)公式需要計算一個L×L矩陣，如果這個矩陣完全顯現(xiàn)在內(nèi)存中，復(fù)雜度為O(L2d),內(nèi)存消耗為O(L2)。右側(cè)公式需要計算一個d×d矩陣，復(fù)雜度為O(Ld2)，內(nèi)存消耗為O(d2)。

隨著上下文長度L的增加,左側(cè)公式的計算成本rapidly become prohibitively非常的高。為了解決這個問題，我們可以考慮移除Softmax。詳細(xì)展開帶有Softmax的公式:

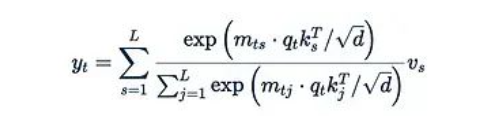
其中：

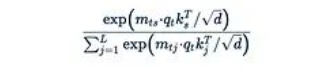
是Softmax函數(shù)。指數(shù)函數(shù)是主要的障礙,它阻止了我們從中提取任何項。如果我們直接移除指數(shù)函數(shù)：

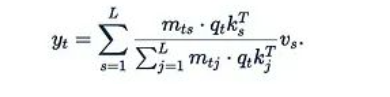
那么歸一化因子

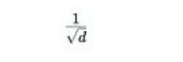
也隨之消失。

這個簡化后的公式存在一個問題:q_t^T k_s不能保證為正,這可能導(dǎo)致值以不同符號的系數(shù)混合,這在理論上是不合理的。更糟糕的是,分母可能為零,會導(dǎo)致計算崩潰。為了緩解這個問題,我們可以引入一個"良好的"元素級函數(shù)φ(稱為核函數(shù)):

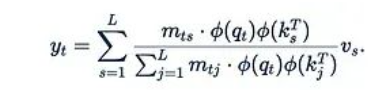
原始研究建議使用φ(x) = 1 + elu(x)作為核函數(shù)。

這種注意力機制的變體被稱為線性化注意力。它的一個重要優(yōu)勢是允許我們利用結(jié)合律:

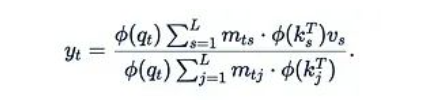
括號中M, K^T和V之間的關(guān)系現(xiàn)在變得相當(dāng)復(fù)雜，不再僅僅是普通的矩陣乘法和元素級乘法。我們將在下一節(jié)詳細(xì)討論這個計算單元。

如果M是一個因果掩碼，即對角線及以下為1，對角線以上為0：

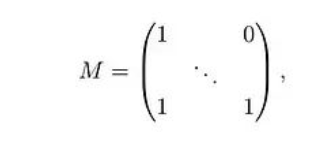
那么計算可以進(jìn)一步簡化：

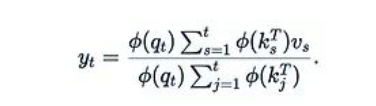
這可以通過一種簡單的遞歸方式計算:

這是在2020年ICML上首次提出線性化注意力的論文"Transformers are RNNs"。在這個公式中，我們有兩個隱藏狀態(tài)：向量z_t和矩陣h_t(φ(k_t)^T v_t是列向量乘以行向量，得到一個d×d矩陣。

而近期的研究often以更簡化的形式呈現(xiàn)線性化注意力，去除了φ函數(shù)和分母:

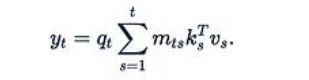
線性化注意力具有兩個主要優(yōu)勢：

● 作為遞歸機制，它在推理時相對于序列長度L具有線性復(fù)雜度。

● 作為Transformer模型，它可以高效地并行訓(xùn)練。

但是你可能會問：如果線性化注意力如此優(yōu)秀，為什么它沒有在所有LLM中廣泛應(yīng)用？我們在討論注意力的二次復(fù)雜度問題？實際上基于線性化注意力的LLM在訓(xùn)練過程中stability較低，且capability略遜于標(biāo)準(zhǔn)自注意力。這可能是因為固定的d×d形狀的瓶頸比可調(diào)整的L×L形狀的瓶頸能傳遞的信息更少。

進(jìn)一步探索

RNN和線性化注意力之間的聯(lián)系在近期的多項研究中得到了重新發(fā)現(xiàn)和深入探討。一個common pattern是使用具有如下更新規(guī)則的矩陣隱藏狀態(tài)：

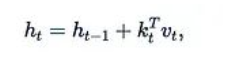
其中k_t和v_t可以視為某種"鍵"和"值"，RNN層的輸出形式為：

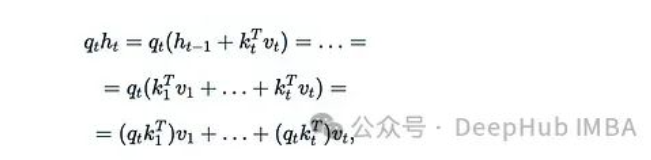
這本質(zhì)上等同于線性注意力。下面兩篇論文提供了有趣的一些樣例：

1、xLSTM (2024年5月)：該論文提出了對著名的LSTM遞歸架構(gòu)的改進(jìn)。其mLSTM塊包含一個矩陣隱藏狀態(tài)，更新方式如下：

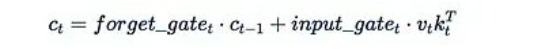
輸出通過將這個狀態(tài)與一個"查詢"相乘得到。(注意：該論文的線性代數(shù)設(shè)置與我們的相反，查詢、鍵和值是列向量而非行向量，因此v_t k_t^T的順序看起來可能有些奇怪。)

2、Learning to (learn at test time) (2024年7月)：這是另一種具有矩陣隱藏狀態(tài)的RNN架構(gòu)，它的隱藏狀態(tài)W是一個函數(shù)的參數(shù)，在t的迭代過程中通過梯度下降優(yōu)化：

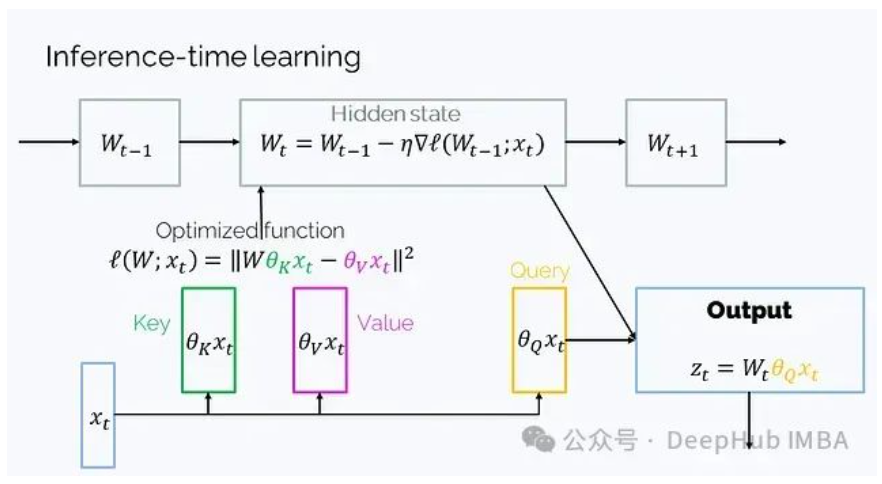
這里的設(shè)置也是轉(zhuǎn)置的，因此順序看起來有些不同。盡管數(shù)學(xué)表達(dá)比W_t = W_{t-1} + v_t k_t^T更復(fù)雜，但可以簡化為這種形式。

以上兩篇論文我們都詳細(xì)介紹過，有興趣的可以自行搜索。

注意力掩碼

在簡化了掩碼注意力機制后，我們可以開始探索其潛在的發(fā)展方向。一個明顯的研究方向是選擇不同的下三角矩陣（確保不會"看到未來"）作為掩碼M，而不是簡單的0-1因果掩碼。在進(jìn)行這種探索之前，我們需要解決由此帶來的效率問題。

在前一節(jié)中，我們使用了一個簡單的0-1因果掩碼M，這使得遞歸計算成為可能。但在一般情況下，這種遞歸技巧不再適用：

系數(shù)m_ts不再相同，也不存在將y_3與y_2關(guān)聯(lián)的簡單遞歸公式。因此，對于每個t我們都需要從頭開始計算總和，這使得計算復(fù)雜度再次變?yōu)長的二次方而不是線性的。

解決這個問題的關(guān)鍵在于我們不能使用任意的掩碼M，而應(yīng)該選擇特殊的、"良好"的掩碼。我們需要那些可以快速與其他矩陣相乘（注意不是元素級乘法）的掩碼。為了理解如何從這種特性中獲益，讓我們詳細(xì)分析如何高效計算：

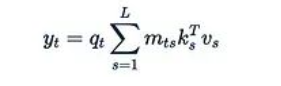
首先明確這個表達(dá)式的含義：

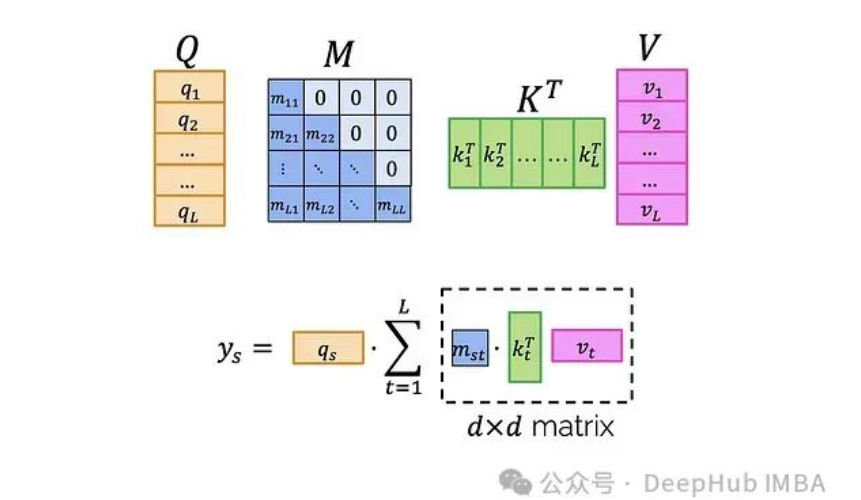
如果深入到單個索引級別：

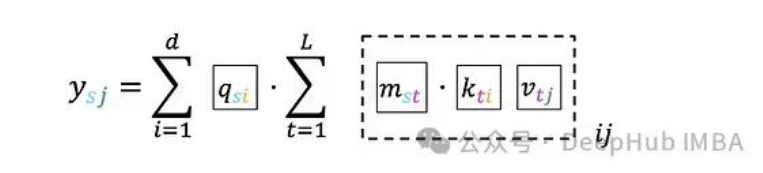
為了便于后續(xù)討論，可以用不同的顏色標(biāo)記索引，而不是塊：

現(xiàn)在我們可以提出一個四步算法：

步驟1. 利用K和V創(chuàng)建一個三維張量Z，其中：

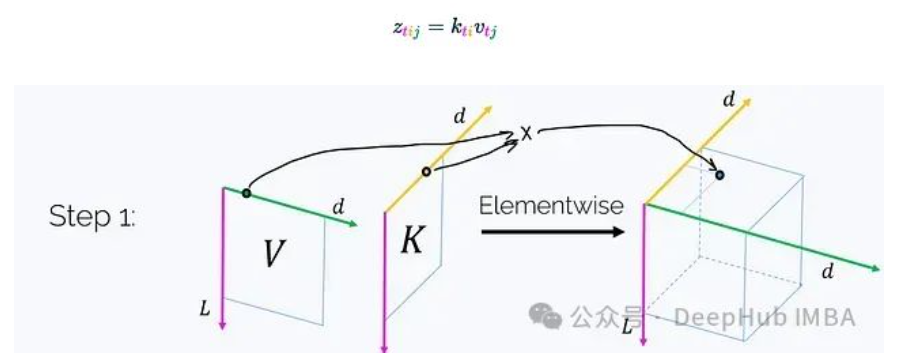
（每個軸都標(biāo)注了其長度。）這一步驟需要O(Ld2)的時間和內(nèi)存復(fù)雜度。值得注意的是，如果我們在洋紅色軸t上對這個張量求和，我們將得到矩陣乘積K^T V：

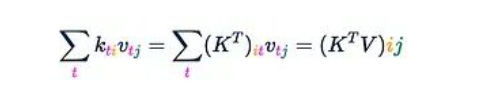
步驟2. 將M乘以這個張量（注意不是元素級乘法）。M乘以Z沿著洋紅色軸t的每個"列"。

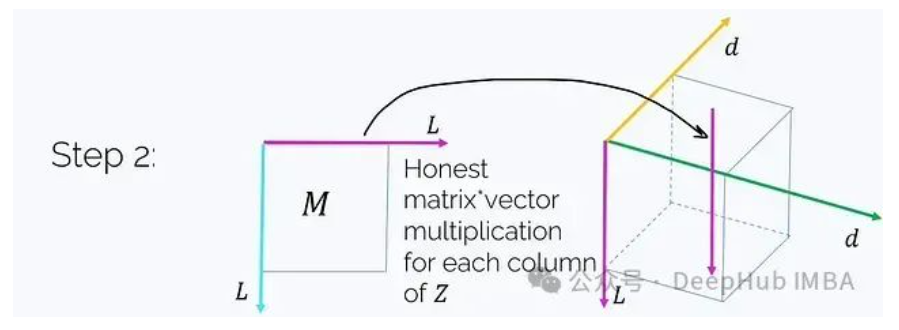
這正好得到：

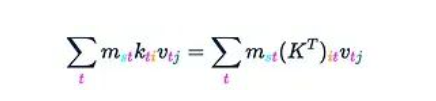
將這個結(jié)果記為H。接下來只需要將所有內(nèi)容乘以q，這將在接下來的兩個步驟中完成。

步驟3a. 取Q并與H的每個j = const層進(jìn)行元素級乘法：

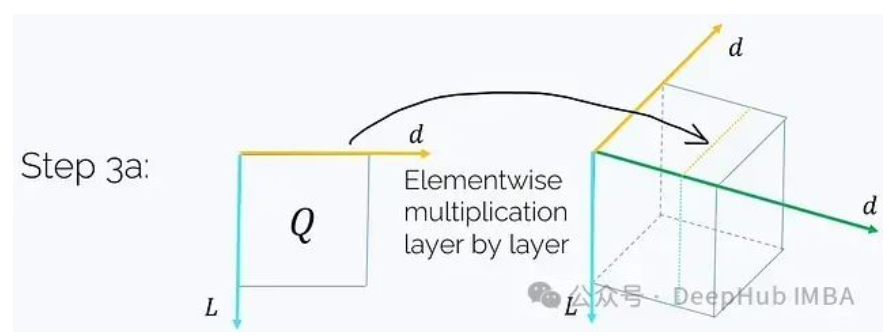
這將得到：

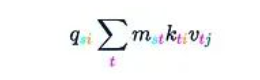
這一步驟需要O(Ld2)的時間和內(nèi)存復(fù)雜度。

步驟3b. 沿i軸對結(jié)果張量求和：

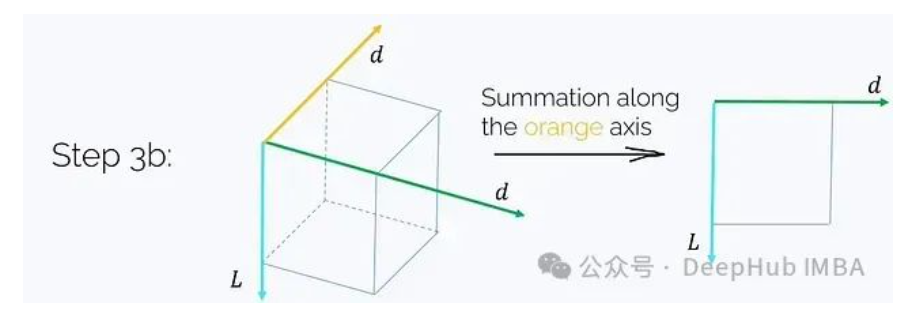
這一步驟同樣需要O(Ld2)的時間和內(nèi)存復(fù)雜度。最終得到了所需的結(jié)果：

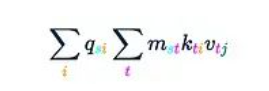
在這個過程中，最關(guān)鍵的是第二步，我們故意省略了其復(fù)雜度分析。一個簡單的估計是：

每次矩陣乘法需要O(L2)的復(fù)雜度，重復(fù)d2次

這將導(dǎo)致一個巨大的O(L2d2)復(fù)雜度。但是我們的目標(biāo)是選擇特殊的M，使得將M乘以一個向量的復(fù)雜度為O(RL)，其中R是某個不太大的常數(shù)。

例如如果M是0-1因果矩陣，那么與它相乘實際上就是計算累積和，這可以在O(L)時間內(nèi)完成。但還存在許多其他具有快速向量乘法特性的結(jié)構(gòu)化矩陣選項。

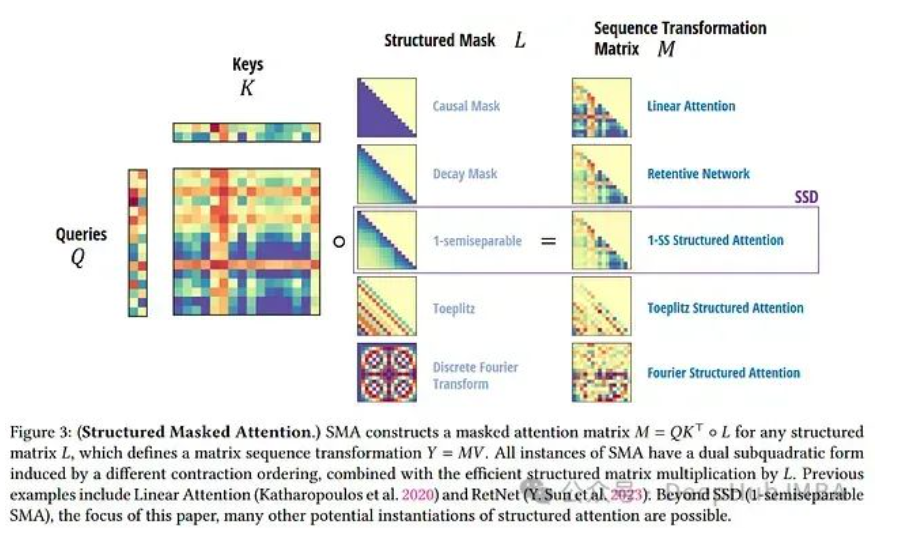
在下一節(jié)中將討論這種矩陣類型的一個重要例子——半可分離矩陣，它與狀態(tài)空間模型有著密切的聯(lián)系。

半可分離矩陣與狀態(tài)空間模型

讓我們回顧一下（離散化的）狀態(tài)空間模型（SSM）的定義。SSM是一類連接1維輸入x_t、r維隱藏狀態(tài)h_t和1維輸出u_t的序列模型，其數(shù)學(xué)表達(dá)式如下：

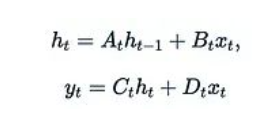
在離散形式中，SSM本質(zhì)上是一個帶有跳躍連接的復(fù)雜線性RNN。為了簡化后續(xù)討論，我們甚至可以通過設(shè)置D_t = 0來忽略跳躍連接。

讓我們將SSM表示為單個矩陣乘法：

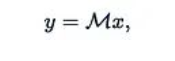
其中

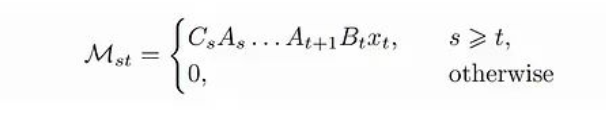
M是一個下三角矩陣，類似于我們之前討論的注意力掩碼。

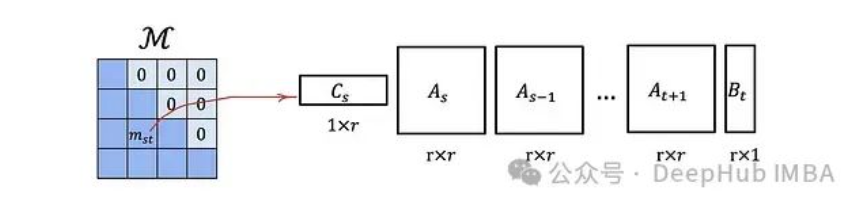
這種類型的矩陣具有一個重要的優(yōu)勢：

一個L × L的下三角矩陣，如果其元素可以以這種方式表示，則可以使用O(rL)的內(nèi)存存儲，并且具有O(rL)的矩陣-向量乘法復(fù)雜度，而不是默認(rèn)的O(L2)。

這意味著每個狀態(tài)空間模型都對應(yīng)一個結(jié)構(gòu)化的注意力掩碼M，可以在具有線性化注意力的高效Transformer模型中使用。

即使沒有周圍的查詢-鍵-值機制，半可分離矩陣M本身已經(jīng)相當(dāng)復(fù)雜和富有表現(xiàn)力。它本身可能就是一個掩碼注意力機制。我們將在下一節(jié)中詳細(xì)探討這一點。

狀態(tài)空間對偶性

在這里，我們將介紹Mamba 2論文中的一個核心結(jié)果。

讓我們再次考慮y = Mu，其中u = u(x)是輸入的函數(shù)，M是一個可分離矩陣。如果我們考慮一個非常特殊的情況，其中每個A_t都是一個標(biāo)量矩陣：A_t = a_t I。在這種情況下公式變得特別簡單：

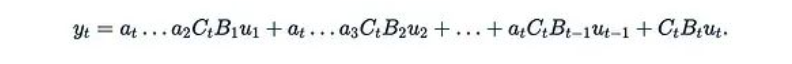
這里的

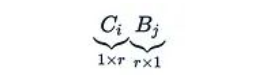
只是一個標(biāo)量。還可以將C_i和B_i堆疊成矩陣B和C，使得：

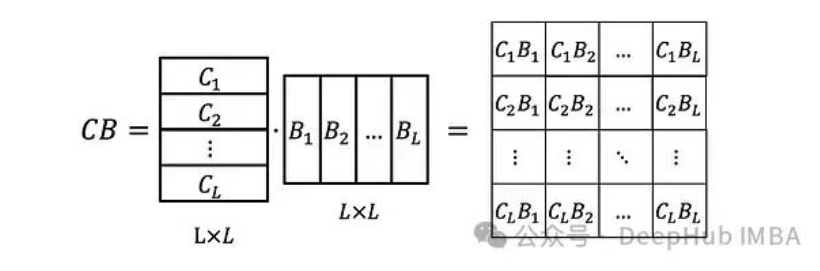
現(xiàn)在我們還需要定義矩陣

然后就可以很容易地驗證：

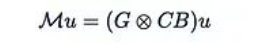
這個表達(dá)式是否看起來很熟悉？這實際上是一個掩碼注意力機制，其中：

● G作為掩碼

● C作為查詢矩陣Q

● B作為轉(zhuǎn)置的鍵矩陣K^T

● u作為值矩陣V

在經(jīng)典的SSM中，B和C是常量。但在Mamba模型中，它們被設(shè)計為依賴于數(shù)據(jù)，這進(jìn)一步強化了與注意力機制的對應(yīng)關(guān)系。這種特定狀態(tài)空間模型與掩碼注意力之間的對應(yīng)關(guān)系在Mamba 2論文中被稱為狀態(tài)空間對偶性。

進(jìn)一步探索

使用矩陣混合器而不是更復(fù)雜的架構(gòu)并不是一個全新的idea。一個早期的例子是是MLP-Mixer，它在計算機視覺任務(wù)中使用MLP而不是卷積或注意力來進(jìn)行空間混合。

盡管當(dāng)前研究主要集中在大語言模型（LLM）上，但也有一些論文提出了用于編碼器模型的非Transformer、矩陣混合架構(gòu)。例如：

● 來自Google研究的FNet，其矩陣混合器M基于傅里葉變換。

● Hydra，除了其他創(chuàng)新外，還提出了半可分離矩陣在非因果（非三角）工作模式下的適應(yīng)性方案。

總結(jié)

本文深入探討了Transformer、循環(huán)神經(jīng)網(wǎng)絡(luò)（RNN）和狀態(tài)空間模型（SSM）之間的潛在聯(lián)系。文章首先回顧了傳統(tǒng)的掩碼自注意力機制，然后引入了線性化注意力的概念，解釋了其計算效率優(yōu)勢。接著探討了注意力掩碼的優(yōu)化，引入了半可分離矩陣的概念，并闡述了其與狀態(tài)空間模型的關(guān)系。最后介紹了狀態(tài)空間對偶性，揭示了特定狀態(tài)空間模型與掩碼注意力之間的對應(yīng)關(guān)系。通過這些分析，展示了看似不同的模型架構(gòu)之間存在深層聯(lián)系，為未來模型設(shè)計和跨架構(gòu)思想交流提供了新的視角和可能性。