利用復(fù)磁導(dǎo)率表征磁芯損耗
在這篇文章中,我們使用磁場強(qiáng)度的概念來幫助解釋復(fù)雜磁導(dǎo)率如何模擬磁芯的損耗。
本文引用地址:http://www.czjhyjcfj.com/article/202405/459387.htm磁導(dǎo)率是用于電氣元件的鐵磁材料的一個關(guān)鍵參數(shù),它將材料內(nèi)部的磁場與外部場聯(lián)系起來。在非常低的頻率下,實(shí)值磁導(dǎo)率可以描述材料的磁化強(qiáng)度。然而,在更高的頻率下,磁性材料制造商使用復(fù)雜的磁導(dǎo)率值。這種復(fù)雜滲透率的想象部分可以解釋巖心損失——但如何解釋呢?
在這篇文章中,我們將深入研究復(fù)磁導(dǎo)率的理論。我們將從研究磁場強(qiáng)度的概念開始討論,這對以后理解一些數(shù)學(xué)知識至關(guān)重要。請注意,當(dāng)我們在本文中提到“磁性材料”時,我們具體指的是鐵磁材料。
磁場強(qiáng)度
本系列先前的文章指出,對于置于均勻磁場(B0)中的材料,材料內(nèi)部的總磁場由下式給出:
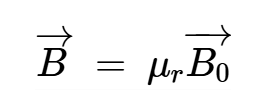
等式1。
其中μr是材料的相對磁導(dǎo)率。
當(dāng)分析磁場對材料的影響時,我們需要不斷區(qū)分B0和B。為了使這種區(qū)分更清楚,我們將定義另一個場量——磁場強(qiáng)度,用H表示。
磁場強(qiáng)度定義為外部施加的磁場除以自由空間的磁導(dǎo)率(μ0):
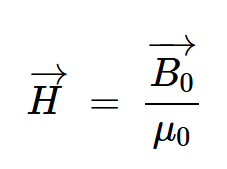
等式2。
使用這個新的場量,方程1可以重寫為:
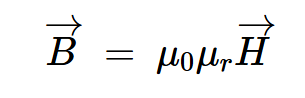
等式3。
乍一看,引入一個新的數(shù)量可能是多余的,但這實(shí)際上是一種方便的方式來澄清我們指的是哪個字段。我們使用H和B字段的特定名稱來強(qiáng)調(diào)它們之間的以下差異:
H是磁場強(qiáng)度(或強(qiáng)度)。
B是磁通密度,有時是磁感應(yīng)。
讓我們來看一個例子。
示例:電磁閥的磁場強(qiáng)度
考慮圖1中的電磁閥。
一個具有N匝和長度為l的示例螺線管。
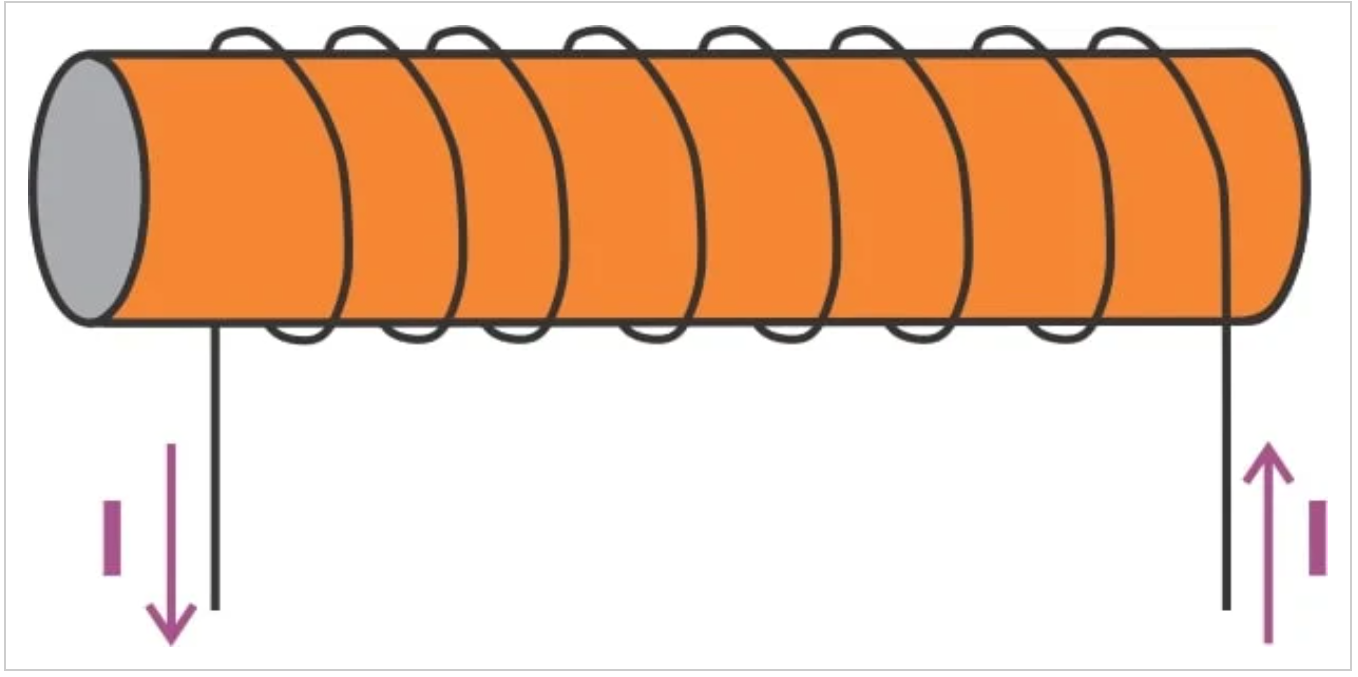
圖1。電磁閥示例。圖片由Steve Arar提供
我們想回答兩個問題:
當(dāng)不使用磁芯時,這個螺線管的磁通密度(B)和磁場強(qiáng)度(H)是多少?
當(dāng)我們插入具有相對磁導(dǎo)率μr的磁芯時,通量密度是如何變化的?
假設(shè)匝間間隔很近,線圈內(nèi)部的場是均勻的,我們可以應(yīng)用安培定律來找到線圈內(nèi)部的電場。在不詳細(xì)介紹這些步驟的情況下,空心螺線管的最終結(jié)果是:
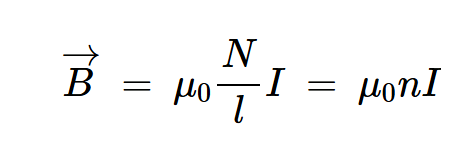
等式4。
解釋
N是總匝數(shù)
l是螺線管的長度
l是電流
n是每單位長度的匝數(shù)。
因?yàn)闆]有使用磁芯,所以方程4中描述的磁場由通過線圈的電流產(chǎn)生,而沒有磁芯磁化的任何貢獻(xiàn)(B=B0)。將該值除以μ0得出磁場強(qiáng)度:
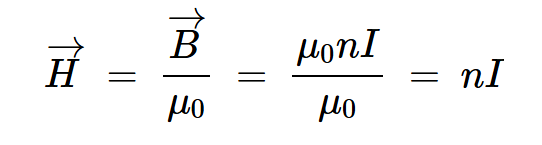
等式5。
如果我們插入一個磁芯,磁通密度變?yōu)椋?/p>
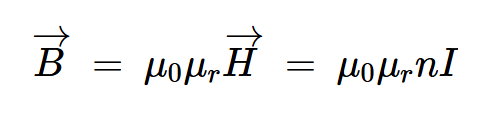
等式6。
由于磁芯的存在,B現(xiàn)在包括兩個磁場分量:
電流產(chǎn)生的磁場。
由核心材料的磁化產(chǎn)生的磁場。
磁場強(qiáng)度本身是由電流產(chǎn)生的,因此可以認(rèn)為是產(chǎn)生磁通密度的驅(qū)動力。滲透率量化了H產(chǎn)生B的容易程度。
磁芯如何改變電感?
接下來,讓我們看看當(dāng)我們插入磁芯時,空心螺線管的電感是如何變化的。電路的電感(L)定義為每單位電流流過電路時通過電路的總磁通量。對于空心螺線管,我們有:
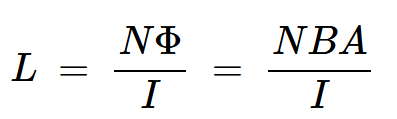
等式7。
解釋
Φ是通過每一圈的磁通量
I是流過線圈的電流
A是電磁閥的橫截面積。
由于沒有磁芯,我們有
→B = μ0→H
.插入磁芯可使磁通密度增加μr。
例如,假設(shè)核心材料的滲透率是自由空間滲透率的500倍。對于給定的電流,使用該磁芯將線圈內(nèi)部的場增加500倍。等式7示出了線圈的電感也以相同的因子增加。
基于以上內(nèi)容,如果空心螺線管的電感為L0,則具有磁芯的同一螺線管的電感將為:
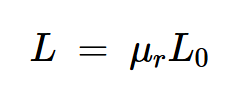
等式8。
現(xiàn)在我們知道了磁芯是如何改變電路電感的,我們可以使用方程8來了解它是如何改變阻抗的。由于理想的空心螺線管充當(dāng)電感為L0的電感器,因此其阻抗為:
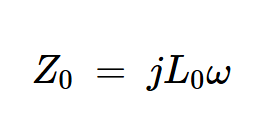
等式9。
當(dāng)插入磁芯時,電感——以及阻抗——乘以相對磁導(dǎo)率,得到:
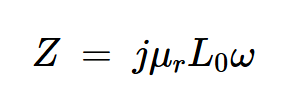
方程式10。
巖心損失的核算:復(fù)雜滲透率
到目前為止,我們已經(jīng)假設(shè)核心是無損的。這就是為什么方程10產(chǎn)生純電感阻抗,我們知道它耗散零平均功率。事實(shí)上,一些輸入能量將作為熱量在堆芯中損失。我們?nèi)绾螌@些核心損失進(jìn)行建模?
注意到電阻器是表示損耗的電氣元件,我們需要一種方法,在上面的阻抗方程中包括一個額外的電阻項(xiàng)。方程中唯一的核心性質(zhì)是滲透率,所以這是我們要修改的參數(shù)。正如你可能已經(jīng)猜到的那樣,我們需要將滲透率定義為一個復(fù)雜的值來解釋巖心損失。復(fù)雜滲透率的方程式為:
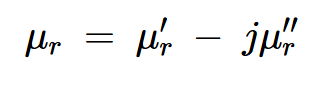
等式11。
通過將復(fù)磁導(dǎo)率代入方程10,我們得到:
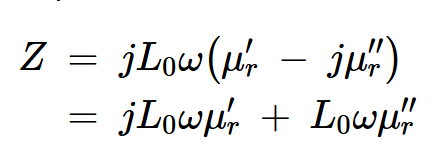
方程式12。
現(xiàn)在,我們的阻抗方程中有兩個不同的項(xiàng):
一個源自磁導(dǎo)率(μr′)實(shí)部的歸納項(xiàng)。這個術(shù)語表明磁芯增加了通過線圈的磁通量,從而增加了其電感。
源自磁導(dǎo)率虛部(μr〃)的電阻項(xiàng)。這個術(shù)語與材料的損失有關(guān)。
方程12得出了圖2所示電感器的等效電路模型,該模型由一個理想的電感器與一個電阻器串聯(lián)組成。
鐵芯損耗串聯(lián)表示的等效電路模型。
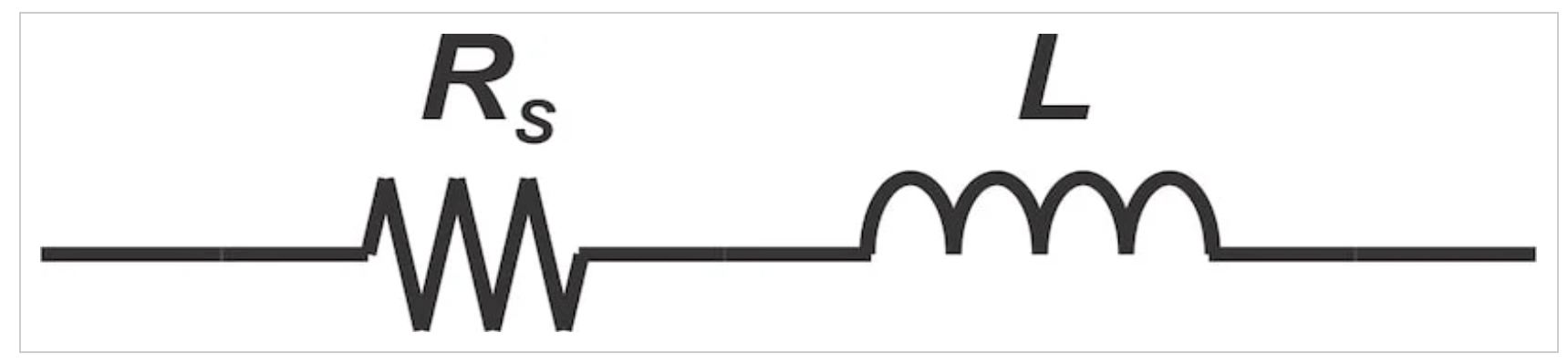
圖2:鐵芯損耗串聯(lián)表示的等效電路。圖片由Steve Arar提供
如果將圖2中的串聯(lián)電路模型轉(zhuǎn)換為其并聯(lián)等效電路,則并聯(lián)電阻也將模擬核心損耗。
磁化與外加磁場異相
我們在方程11中定義了復(fù)磁導(dǎo)率。讓我們看看這個等式到底意味著什么。
我們知道,磁導(dǎo)率描述了施加在磁性材料上的外部場與其內(nèi)部產(chǎn)生的場之間的關(guān)系。方程11中磁導(dǎo)率的實(shí)部對應(yīng)于與外部場同相的材料磁化。這是我們對理想無損內(nèi)核的期望。
另一方面,磁導(dǎo)率的虛部表明,材料的某些磁化與所施加的場發(fā)生90度異相。這種相移導(dǎo)致電感器兩端的感應(yīng)電壓與流過電路的電流同相,從而在整個阻抗方程中產(chǎn)生電阻項(xiàng)。
圖3顯示了兩個不同核心的B和H場之間的相位關(guān)系。圖3(a)對應(yīng)于無損核心,圖3(b)對應(yīng)于有損核心。
B和H之間的相位關(guān)系。
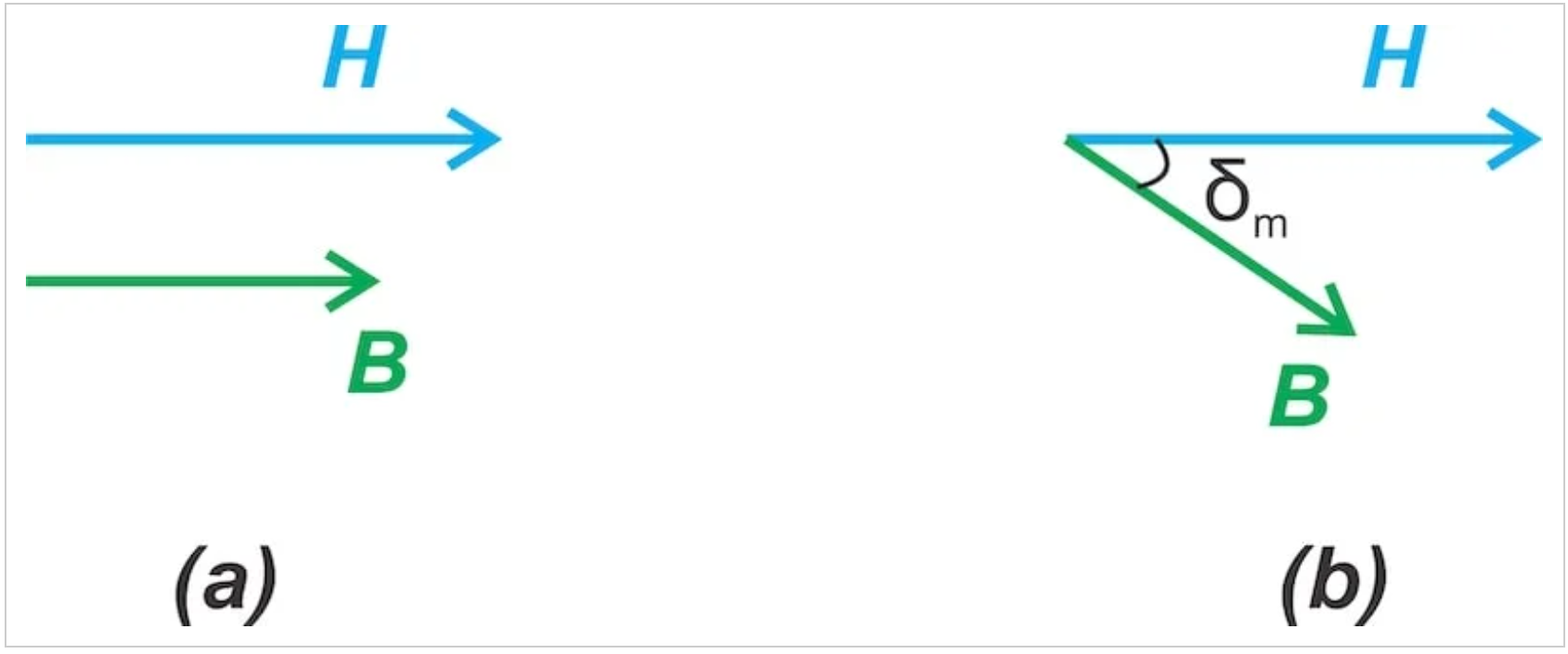
圖3。B場和H場之間的相位關(guān)系。圖片由Steve Arar提供
在無損核心中,
→B



















評論