混合靈敏度H∞控制在平臺穩定回路上的應用
0 引言
如今,隨著網絡信息技術的迅猛發展,以及人們對力學、電學等理工學科研究的不斷深入,慣性導航技術也在隨之發生著日新月異的變化。在慣性導航系統中,控制技術起著至關重要的作用,目前平臺式慣導控制大多采用經典頻域控制設計方法。隨著控制技術的發展,魯棒控制理論也得到了極大的發展,它對于控制對象存在不確定性和結構攝動有更好的控制效果。本文采用魯棒H∞控制對平臺穩定回路進行控制,通過選擇適當的權函數將平臺穩定回路控制問題轉化為H∞ 混合靈敏度問題,運用混合靈敏度優化設計出了一個滿足性能要求的控制器,并通過特殊的雙線性變換方法,解決了平臺穩定回路原系統對象模型有位于虛軸極點這一病態問題。最后,通過仿真驗證了控制器的可行性。
1 液浮陀螺平臺穩定回路的原理
三軸慣性平臺具有三條伺服回路通道,其原理基本相同。當某一干擾力矩M f 作用在平臺臺體框架軸上時,平臺將相對慣性空間產生轉動,液浮陀螺敏感到此偏轉角度后,輸入相應的調寬信號,經過放大器放大后反饋到控制裝置,由控制裝置產生控制信號作用在穩定電機上,穩定電機產生相反方向的修正力矩,帶著平臺向著原來偏離的反方向運動,使平臺與慣性空間的夾角逐漸減小到0,最終使平臺相對于慣性空間保持穩定。
2 平臺穩定回路建模
2.1 穩定回路的組成
一般穩定回路由慣性平臺、三環框架、安裝在平臺上的陀螺儀、力矩電機、坐標變換器和控制電路組成。具體組成如圖1 所示,其中Md 為力矩電機扭轉力矩,Mf為穩定回路外部干擾力矩。圖1 由橫滾穩定回路和俯仰穩定回路組成,方位穩定回路沒有耦合放大器和伺服分解器兩個環節。
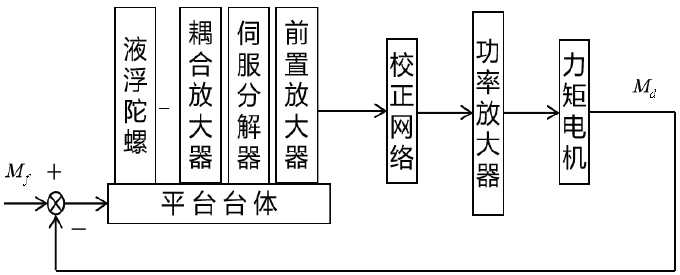
圖1 平臺穩定回路組成
2.2 穩定回路的數學模型
圖2 為方位穩定回路控制框圖,其中,θ ′ 為穩定回路輸入角度,θ 為陀螺輸出角,k1 為橋式功率放大系數,k2 為傳感器、前置放大、相敏解調和低通濾波放大系數、τ g 為陀螺時間常數、kg 為陀螺傳遞系數、τ e 為電機時間常數, J 為平臺轉動慣量。不考慮校正裝置,穩定回路的開環傳遞函數為
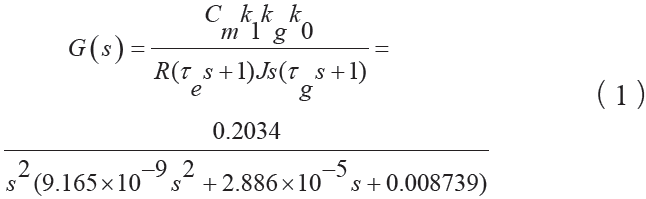
3 常規PID控制
PID 控制器是控制系統中最常使用的一種控制器,具有結構簡單、調整方便、穩定性好及工作可靠等優點。PID 控制主要依靠被控系統的輸出值與目標值之間的偏差和實際經驗來實現系統的控制。平臺穩定回路通常采取雙閉環控制,即電流環PI 控制、位置環PID 控制,控制框圖如圖2 所示。
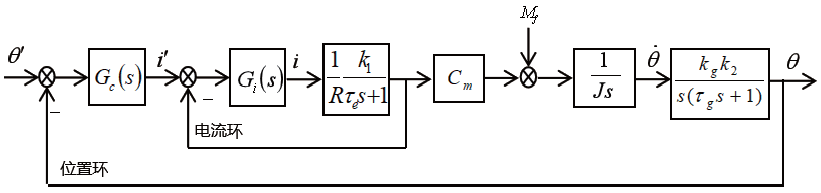
圖2 方位穩定回路雙閉環控制
3.1 電流環PI控制
電流環反饋能夠自動調節力矩電機的驅動電流,大大減小載體角運動和干擾力矩引起的力矩電機輸出力矩波動,從而提高系統性能。
未校正前電流環開環傳遞函數為
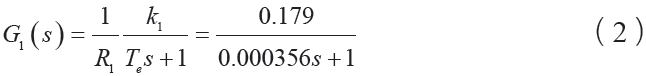
采用PI 實現電流環控制,控制器的傳遞函數如下形式:

根據工程的實際情況,此處取電流環的開環截止頻率為 1 800~2 000 rad / s,此時取電流環校正函數為
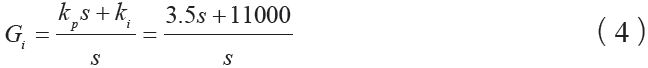
可得電流環閉環傳遞函數為
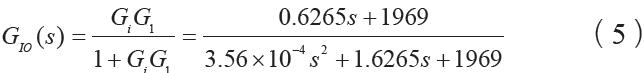
為計算方便,忽略分子、分母的高階系數項,將上式簡化為一階環節,得到式:

加入校正環節后,電流環的開環bode 圖如圖3所示。
控制后開環系統的截止頻率為 1 910 rad / s,相位裕度為87.1°。
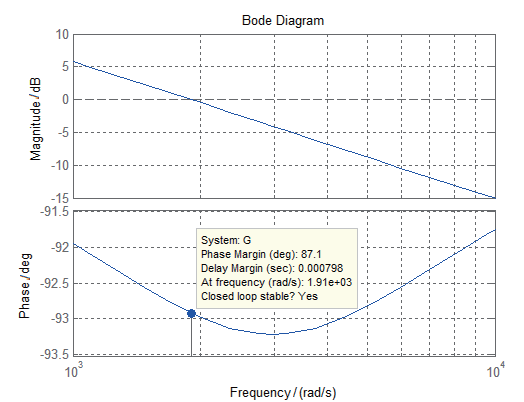
(a)控制后電流環bode圖
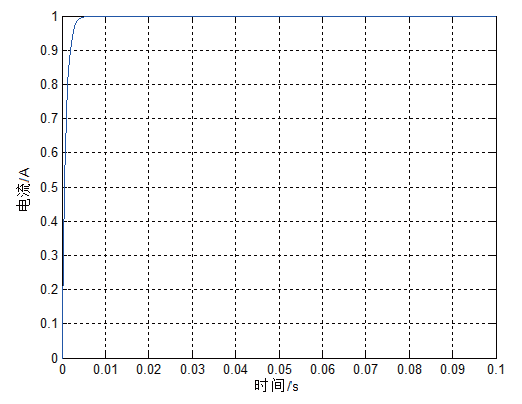
(b)電流環單位階躍響應
圖3 電流環的開環bode圖
3.2 位置環PID控制
PID 控制采用比例- 積分- 微分控制的基本形式。本文位置環PID 校正整定采取臨界比例法。
對PID 控制穩定環回路輸入0.1 rad 的階躍信號和0.5 N·m 的干擾力矩,系統的響應曲線如圖4 所示。
從圖4 可以看出,采用常規PID 控制后,系統超調為18.5%,調節時間為0.12 s,當輸入常值干擾力矩后,穩定回路的最大動態干擾誤差為0.014 9 rad,穩定誤差最終趨于0。
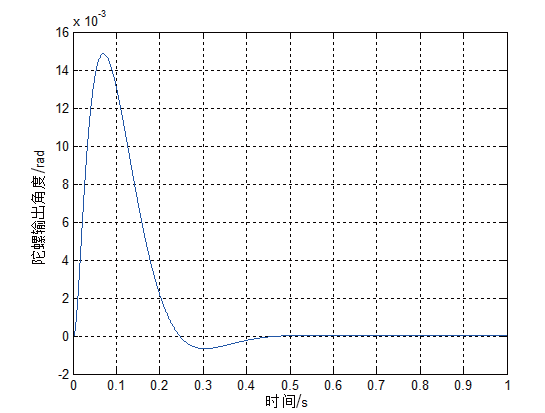
(a)階躍響應下陀螺輸出
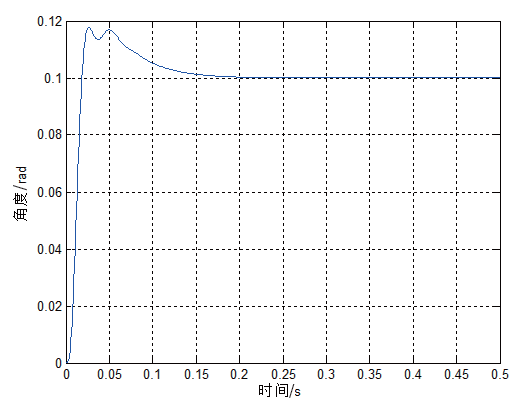
(b)干擾力矩下陀螺輸出
圖4 系統響應的曲線圖
4 H∞混合靈敏度設計問題
控制混合靈敏度優化目前運用廣泛的設計方法,它可以將系統的魯棒穩定性和性能要求轉化為H∞ 標準設計問題,再采用DGKF 方法,通過求解一個或兩個Riccati 方程,求解出控制器。
混合靈敏度加權的控制結構如圖5 所示,其中r 為參考輸入、e 為跟蹤誤差、u 為控制輸入、d 為干擾輸入、y為系統輸出、G(s)為控制對象、W1、W2、W3為權函數、K (s )為控制器。r對e、u、y的傳遞函數分別為
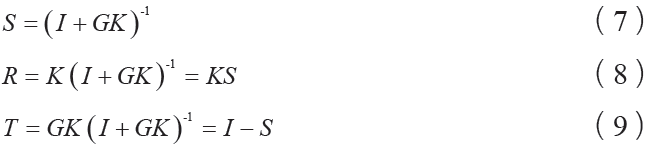
其中, S 和T 分別被稱為靈敏度函數和補靈敏度函數,二者滿足:T (s) = I ? S (s)。靈敏度函數S (s)是決定跟蹤誤差大小的重要指標,S (s)增益越低,系統的跟蹤誤差越小,故系統響應的品質指標越好;而補靈敏度函數T (s)是決定系統魯棒穩定性的重要指標,降低T (s)增益可以減小模型不確定性對系統的影響。但由于T (s) = I ? S (s),不可能同時降低S和T的增益,通常干擾信號多為低頻信號,系統不確定性發生高頻,因此在選擇權函數上可以對二者進行分頻段折衷。
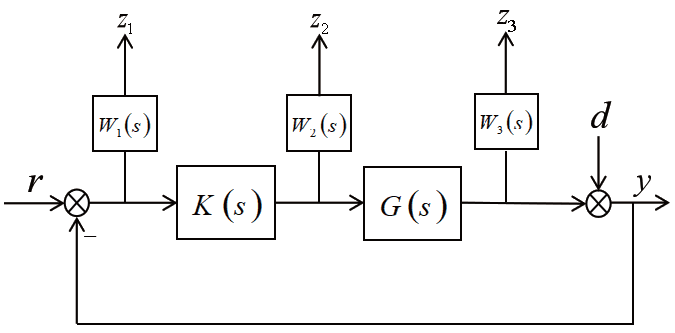
圖5 混合靈敏度控制框圖
由圖5 所示,干擾d 到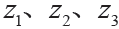 的傳遞函數分別為
的傳遞函數分別為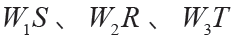 ,混合靈敏度問題的框架為
,混合靈敏度問題的框架為
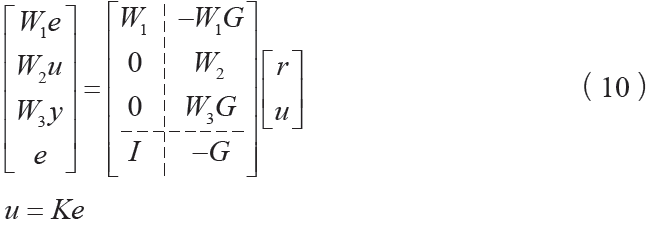
其中,增廣對象模型為

簡單推導可得,
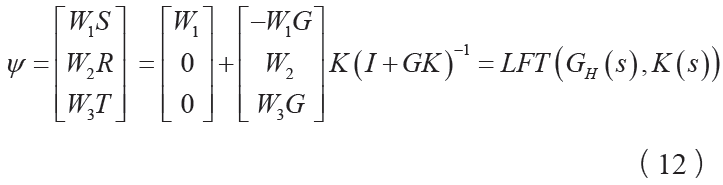
上式右端為目標函數的線性分式變換形式。因此,使系統內部穩定且滿足設計指標ψ ∞ <1的控制器K (s)的問題,就可以歸結為求增廣被控對象G s H( )所對應的H∞ 標準設計問題,解K (s)的問題。
在本文中,圖5中的G(s)即為力矩電機、平臺臺體、液浮陀螺三者組成的總被控對象,代入具體數值:
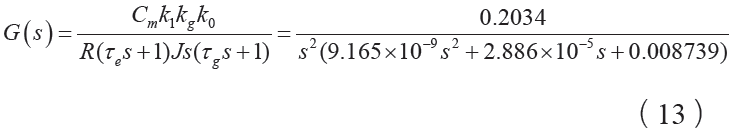
按照圖5 混合靈敏度控制結構,設給定信號為0,可將圖2 等效變換為H∞標準控制結構,如圖6 所示。虛線框即為增廣對象,它包含原控制對象 G(s) W1 、W2 、W3 三個權函數。
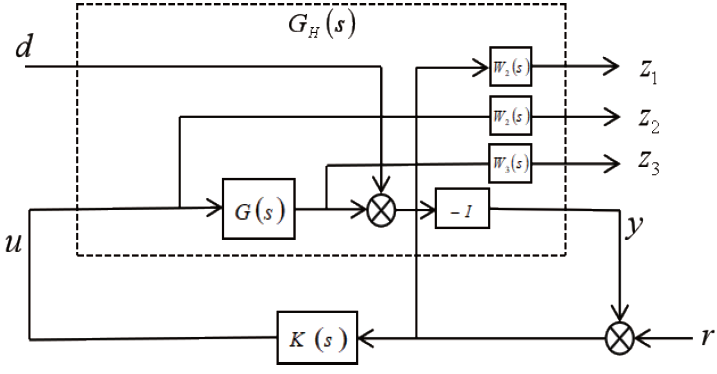
圖5 方位穩定回路H∞標準控制結構圖
5 混合靈敏度H∞控制器的設計
5.1 權函數的選擇
應用混合靈敏度方法設計控制器時,加權陣的選取是重中之重,它決定了系統靈敏度函數和補靈敏度函數頻域特性的形狀,進而直接決定了整個系統動態、穩態性能及魯棒性的好壞。加權陣的選取需要遵循以下規則:
1)最終設計的控制器和廣義被控對象同階,因此在滿足設計要求的情況下,盡量降低加權陣的階次。
2)靈敏度函數S (s)決定了系統的跟蹤性能,它越小表明系統抑制擾動能力越強,系統的跟蹤性能越好,
由于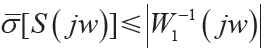 ,因此
,因此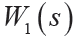 截止頻率應在低頻段且滿足低通高增益。
截止頻率應在低頻段且滿足低通高增益。
3) 為控制量限制權函數,為了不增加控制器階次通常選擇一常數。
為控制量限制權函數,為了不增加控制器階次通常選擇一常數。
4)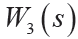 為對象不確定性界函數,它決定了系統魯棒邊界,其幅頻特性包含所有未建模動態,而未建模動態往往呈高頻特性,因此其要求在低頻增益小,高頻增益大,并且其截止頻率需大于
為對象不確定性界函數,它決定了系統魯棒邊界,其幅頻特性包含所有未建模動態,而未建模動態往往呈高頻特性,因此其要求在低頻增益小,高頻增益大,并且其截止頻率需大于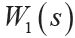 截止頻率。
截止頻率。
根據以上規則,反復試湊,最終選定
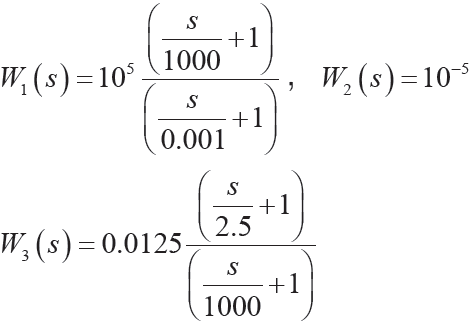
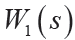 和
和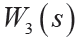 的幅頻曲線如圖6 所示。從圖中可以看出設計的權函數較好滿足了
的幅頻曲線如圖6 所示。從圖中可以看出設計的權函數較好滿足了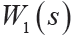 的高增益低通和
的高增益低通和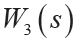 的高通濾波特性。
的高通濾波特性。
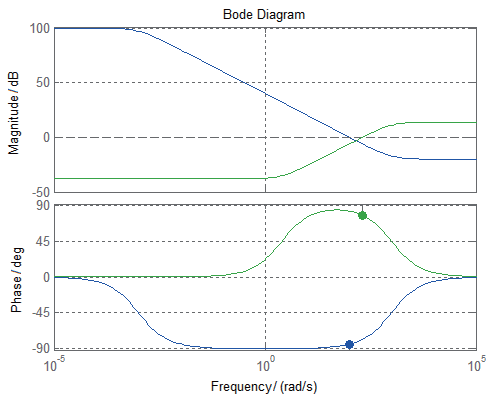
圖6 權函數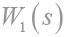 和
和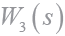 的幅頻曲線
的幅頻曲線
5.2 H∞控制器的設計
本文的控制對象傳遞函數存在虛軸上的極點,故在設計H∞ 控制器的時候需先進行雙線性變換將虛軸極點移位,待設計好后在將以為極點還原,最終運用MATLAB 魯棒控制工具箱中的hinfsyn 函數,得到的魯棒控制器的形式為:
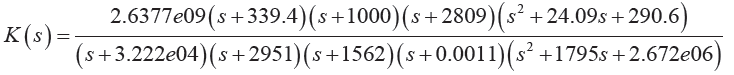
圖 7(a)(b) 分別給出了描述系統靈敏度函數S(s)和權函數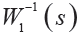 、補靈敏度函數T (s) 與權函數
、補靈敏度函數T (s) 與權函數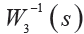 與頻率ω 關系的奇異值曲線。
與頻率ω 關系的奇異值曲線。
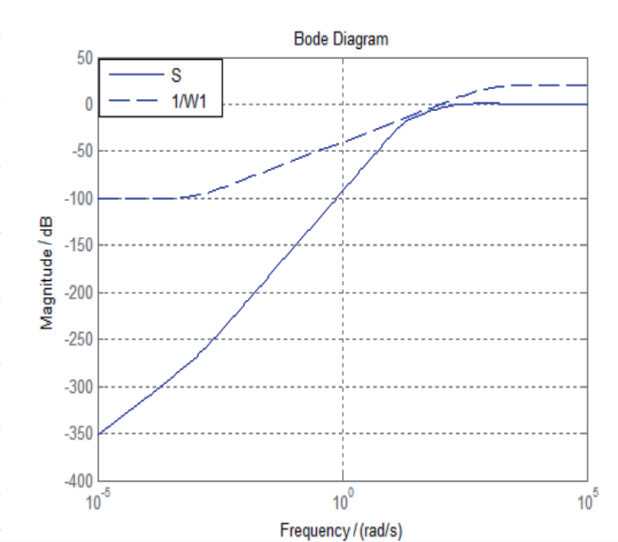
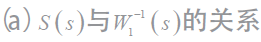
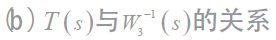
圖7 奇異值曲線
WS 1 代表對系統跟蹤和干擾抑制性能的要求,應滿足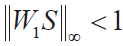 這一必要條件,即
這一必要條件,即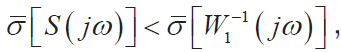 從圖7(a) 中可以看出,所設計控制器滿足系統性能要求。W3T代表對系統魯棒穩定性的要求,應滿足
從圖7(a) 中可以看出,所設計控制器滿足系統性能要求。W3T代表對系統魯棒穩定性的要求,應滿足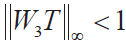 這一必要條件,即滿足
這一必要條件,即滿足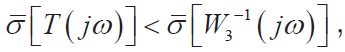 從圖7(b) 中可以看出,從圖中可以看出補靈敏度函數在高頻段受到抑制,所設計的控制器滿足系統性能的要求。
從圖7(b) 中可以看出,從圖中可以看出補靈敏度函數在高頻段受到抑制,所設計的控制器滿足系統性能的要求。
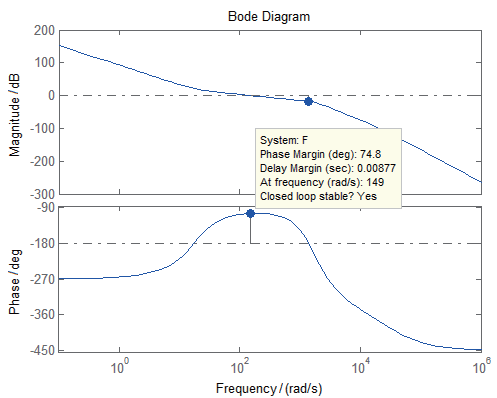
圖8 H∞控制下的系統開環傳遞函數曲線
從圖8 中可以看出,系統的截止頻率ωc =149 rad / s,相位裕度為74.8°,滿足精度和魯棒穩定性要求。低頻段系統表現為-60 dB/dec,這說明系統對階躍響應必為無靜差系統,具有很好的穩定性,并且由于系統低頻段有較高的分貝值,可以保證系統的穩態精度;中頻段以-20 dB/dec 穿過0 dB 線且具有一定的寬度,從相位裕度也可以看出系統有較好的平穩性;在高頻段系統表現為-60 dB/dec,這表明系統有較好的噪聲抑制能力。
(a)階躍響應下陀螺輸出
(b)干擾力矩下陀螺輸出
圖9 系統響應曲線
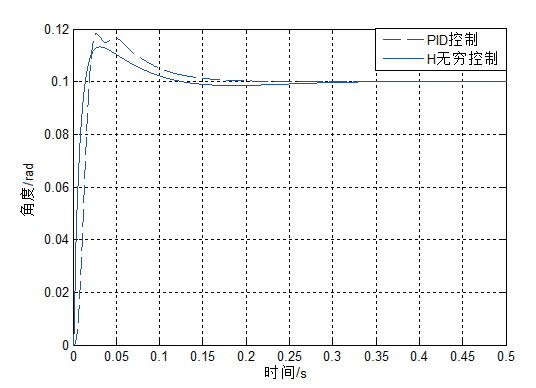
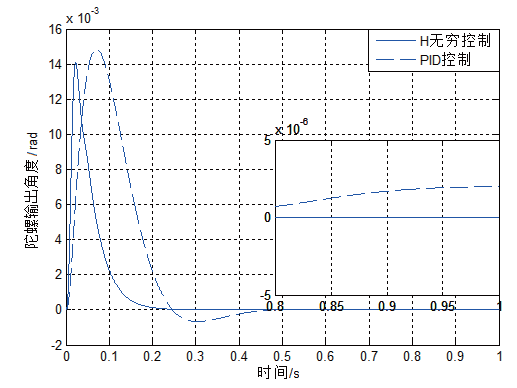
對H∞控制穩定回路輸入0.1 rad的階躍信號和0.5 N·m 的干擾力矩,系統的響應曲線如圖9 所示。
從圖9 可以看出,采用H∞ 控制后,系統的超調量僅為13.7%,調節時間僅為0.089 s,當輸入常值干擾力矩后,穩定回路的最
大動態干擾誤差為0.013 7 rad, 穩態誤差趨于0。通過PID 控制和H∞ 控制的對比,可以看出,系統的超調量超調量、調節時間和抗干擾能力都明顯得到了明顯改善。
6 結語
本文應用H∞ 混合靈敏度控制策略對液浮陀螺穩定回路進行控制,通過選擇合適的加權函數,使控制結果在跟蹤和抗擾方面都有了顯著的提高,通過仿真,驗證了采用H∞ 控制器的穩定回路較傳統PID 雙環控制器的穩定回路具有更好的跟蹤性能和抗擾性能,從而證實了此方法的有效性。
參考文獻:
[1] 秦永元.慣性導航[M].北京:科學出版社,2006.
[2] 申鐵龍.H∞控制理論及應用[M].北京:清華大學出版社,1996.
[3] 薛定宇.控制系統計算機輔助設計-MATLAB語言及應用[M].北京:清華大學出版社,2012.
[4] 劉金琨.先進PID控制MATLAB仿真[M].3版.北京:電子工業出版社,2011.
[5] 吳旭東,解學書.H∞魯棒控制中的加權矩陣的選擇[J].清華大學學報(自然科學版),1997:29-32.
[6] 李鵬,孟衛鋒,陳利超,等.慣導平臺穩定回路三種控制策略的仿真研究[J].科學技術與工程,2010(3):672-676,691.
(本文來源于《電子產品世界》雜志2021年1月期)


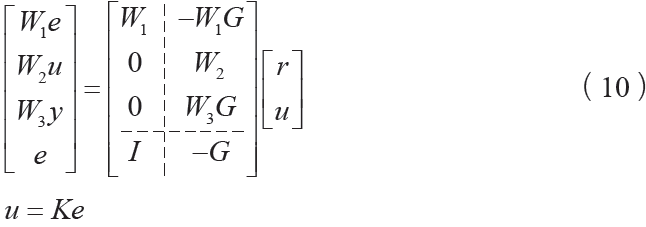
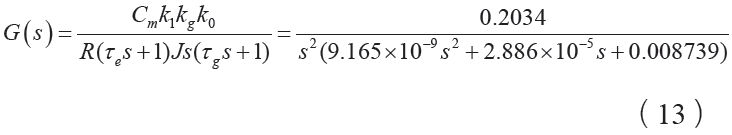
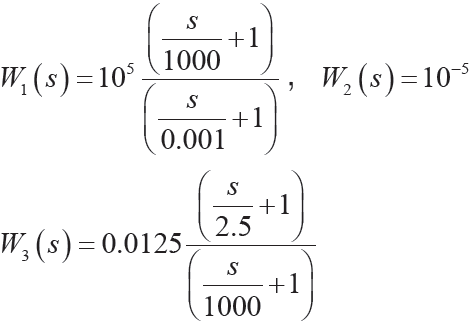






評論