基于重復控制的雙DSP+FPGA三相逆變器

基于雙DSP+FPGA的三相逆變器的設計與實現

三相逆變器作為現在一種常用的電力電子設備，對輸出電壓控制系統需同時實現兩個目標:高動態響應和高穩態波形精度。諸如PID、雙閉環PID、狀態反饋等控制方案，雖然能實現高動態特性，但是不能滿足高質量的穩態波形。

本文利采用雙閉環PI和重復控制相結合的控制方案，首先用雙閉環PI控制算法，得到高動態特性的三相交流電，不過不能滿足高質量的穩態波形，因為用電壓質量要求比較高的非線性負載———鎮流器是電感式的鈉燈作為三相逆變器的負載時，鈉燈不能穩定的工作(會高頻率地閃爍)，針對這一問題，在雙閉環PI的基礎上加重復控制補償，建立MATLAB 仿真，并在雙DSP+FPGA 硬件架構中高效精確的實現。實驗結果表明，加上重復控制補償后，鈉燈能夠穩定的工作，三相逆變器的穩態性能得到了很大的改善。

1 三相逆變器數學模型的建立

三相LC逆變器的主電路拓撲如圖1，組成部分主要有三相逆變橋、三相濾波電感L、三相濾波電容C 。

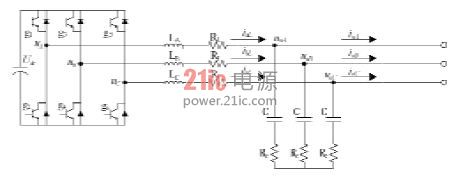
圖1 LC 三相逆變器的主電路拓撲

定義三相逆變器負載側輸出電壓為uoA、uoB、uoC，輸出電流為ioA、ioB、ioC，三相逆變器電感L 側輸入電壓為uA、uB、uC，輸出電壓為uoA、uoB、uoC，流過電感的電流為iaL、ibL、icL。

以電感電流和輸出電壓為狀態變量，建立在三相靜止坐標系中的狀態空間表達式如下。

狀態方程為:

輸出方程為:

dk-調節器輸出的調制信號。

以上為三相逆變器的靜止坐標系中的數學模型，下面討論其解耦模型。

引入如下三相靜止坐標系到兩相靜止坐標系的變換關系式:

將式(3)代入式(1)，即可得到在兩相靜止坐標系下控制對象的傳遞函數表達式如下:

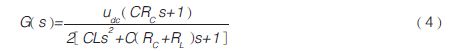
從上面的控制對象的傳遞函數表達式可知，α軸和β軸已經完全解耦，各自等效為單相半橋逆變器。

從上面的分析可以看到:①在兩相靜止坐標系下，三相逆變器是完全解耦的，可等效為兩個單相半橋逆變器。②三相解耦后的模型與單相逆變器模型相同，所以三相逆變器的控制的分析與設計方法可以借鑒單相逆變器。