全新CMRC寬帶低通濾波器設計

濾波器在通信、軍事、測試測量等領域應用廣泛，尤其在近幾年的在微波及毫米波電路中有著廣泛的應用。在低頻段的應用中， 集總參數濾波器有著良好的表現，但是隨著頻率升高到微波頻段以上，集總參數元件(電容、電感)的Q值急劇下降，造成濾波器的插入損耗太大，這時就必須用分布參數元件來代替集總參數元件，但是分布參數元件濾波器的尺寸一般較大，因此有必要減小微波毫米波電路濾波器的尺寸。

2000年香港城市大學薛泉教授提出了一種緊湊的微帶諧振器(CMRC)，此后螺旋緊湊微帶諧振器(SCMRC)以及直線緊湊微帶諧振器(BCMRC)又相繼被提出。然而 SCMRC結構的阻帶范圍較小(5.2GHz-7.6GHz)，BCMRC則由于在阻帶范圍內的衰減特性不理想通常需要幾個單元來實現較好的低通特性。針對這些問題，本文提出了一種新型CMRC寬帶低通濾波器， 在0-7GHz低通頻率范圍內其最大插入損耗為0.3dB,低于-10dB的阻帶頻率范圍為8.5GHz-22.1GHz, 低于-20dB阻帶頻率范圍為9GHz-20.8GHz,可見該濾波器在通帶內具有很低的插入損耗，并且在阻帶內具有良好的衰減特性。

結構與等效電路

本文提出的新型CMRC平面結構如圖1所示，其LC等效電路模型如圖2所示。介質基板采用Taconic CER_10，其介電常數er=9.5,厚度0.64mm。

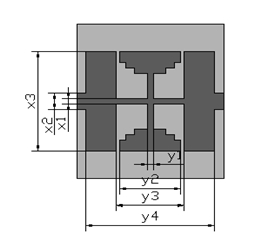
圖1、CMRC的平面結構

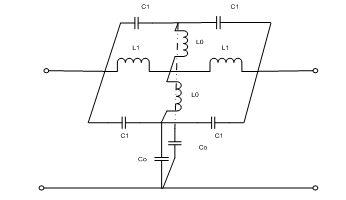
圖2、LC等效電路模型

濾波器特性仿真分析

1、主要結構參數對傳輸特性的影響

我 們對圖1所示CMRC結構應用HFSS進行建模以及仿真，并分析了主要結構參數對濾波器傳輸特性的影響。在仿真中我們發現x1、y1以及y2對濾波器傳輸 特性的影響較大，其影響特性曲線如圖3至圖5所示，由圖3和圖4可知減小x1和y1可以降低諧振頻率，從而相應的可以減小低通頻率范圍，這是因為在等效電 路模型中，減小x1或y1都可以提高單位長度的分布串聯電感(L0和L1)。而諧振頻率，可知L0和L1的增大會相應的降低諧振頻率。

圖5所示為y2大小對傳輸系數的影響，y2的數值越接近y3，諧振頻率越低。這是因為增大y2可以提高該微帶部分的單位長度分布電容，另外縫隙的減小同時增大了邊沿耦合電容，從而導致其等效電容C1的增加，進而降低其諧振頻率，減小低通頻率范圍。

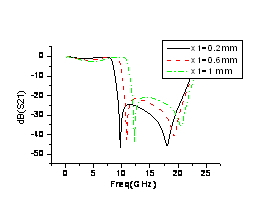
圖3、傳輸系數隨結構參數x1變化特性

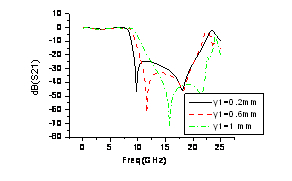
圖4、傳輸系數隨結構參數y1變化特性

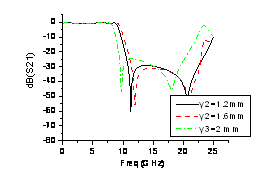
圖5、傳輸系數隨結構參數y2變化特性

2、優化結果及其主要參數

經 上述分析，對該CMRC寬帶低通濾波器進行優化，得到了良好的輸出S參數特性曲線如圖6所示，在0到7GHz低通頻率范圍內的最大插入損耗為0.3dB, 低于-10dB的阻帶頻率范圍為8.5GHz-22.1GHz, 低于-20dB的阻帶頻率范圍為9GHz-20.8GHz，可見該寬帶低通濾波器具有良好的低通及阻帶衰減特性。此時主要微帶分布參數由表1給出。

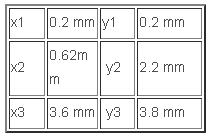
表1、主要微帶結構參數

該濾波器在寬通帶范圍內插入損耗很低，并且在寬阻帶范圍內具有很好的衰減特性，可用于高中頻混頻器的中頻濾波器，并可以有效的抑制本振及其諧波成分。另外該寬帶低通濾波器尺寸很小，具有容易集成的優點。