淺析基于DSP的癲癇腦電信號處理原理與應用

1引 言

癲癇的診斷主要依靠臨床病史，腦電圖檢查可作為一種極有價值的輔助診斷手段。據統計，80%左右的癲癇病人都具有確定性的腦電異常，而只有5～20%左右的癲癇病人腦電圖表現正常。尤其對臨床診斷困難的非典型癲癇發作、各種異型癲癇和隱匿型癲癇，腦電圖檢查的重要性更加突出，甚至起著決定性的作用[1]。

腦電（EEG）是超高斯或亞高斯信號，通常都含有噪聲、偽跡和串擾。通常，腦電活動總體上被劃分成4個頻帶成分（β，α，θ和δ等節律），這些成分的頻率都很低（在0.5～40 Hz范圍）。而臨床分析表明癲癇患者發病時以3 Hz棘慢綜合波為多見。換句話說，腦電中有意義的成分基本上都是低頻信號。這意味著，我們可以通過小波分解將混迭在腦電中的高頻成分濾除后再重構，從而濾除噪聲和偽跡。通過研究癲癇病人的腦電信號，有助于藥物選擇、劑量調整和藥物停用的決定，有助于外科手術治療病例的選定，有助于癲癇和其他發作性疾病的鑒別。

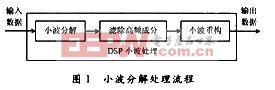
實現流程如圖1所示。

2離散小波變換算法

離散小波變換的一個突破性成果是S.Mallat于1989年在多分辨分析的基礎上提出的快速算法一一Mallat算法[2]。Mallat算法在小波分析中的作用相當于快速傅里葉變換（FFT）在傅里葉分析中的作用，他標志著小波分析走上了寬闊的應用領域。Mallat算法又稱為塔式算法，他由小波濾波器H，G和h，g對信號進行分解和重構[3]。分解算法為：

式中，t為離散時間序列號，t=1，2，…，N;f（t）為原始信號；j為層數或小波尺度，j=1，2，…，J，J=log2N;H，G

為時域中的小波分解濾波器，實際上是濾波器系數；Aj為信號f（t）在第j層的逼近部分（即低頻成分）的小波系數；Dj為信號f（t）在第j層的細節部分（即高頻部分）的小波系數。

式（1）的含義是：假定所檢測的離散信號f（t）為A。信號，信號f（t）在第2j尺度（第j層）的近似部分，即低頻部分的小波系數Aj是通過第2j-1尺度（第j-1層）的逼近部分的小波系數Aj-1與濾波器H卷積，然后將卷積的結果隔點采樣得到的；而信號f（t）在第2j尺度（第j層）的細節部分，即高頻部分的小波系數Dj是通過第2j-1尺度（第j-1層）的逼似部分的小波系數與分解濾波器G卷積，然后將卷積的結果隔點采樣得到的。

通過式（1）的分解，在每一尺度2j上（或第j層上）信號f（t）被分解為近似部分的小波系數Aj（在低頻子帶上）和細節部分的小波系數D，（在高頻子帶上）。

重構算法為：

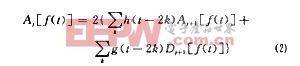
式中，j為分解的層數，若分解的最高層即分解的深度為J，則j=J-1，J-2，…，1，0;h，g為時域中的小波重構濾波器，實際上是濾波器系數。

式（2）的含義是：信號f（t）在第2j尺度（第j層）的近似部分的小波系數，即低頻部分的小波系數Aj是通過第2j+1尺度（第j+1層）的逼近部分的小波系數Aj+1隔點插零后與重構濾波器h卷積以及第2j+1尺度（第j+1層）的細節部分的小波系數Dj+1隔點插零后與重構濾波器g卷積，然后求和得到的。不斷重復這一過程，直到第2°尺度，得到重構信號。

3小波變換的DSP實現

3.1 腦電信號在CCS 2.2上的輸入與輸出

CCS 2.2（Code Composer Studio）是由TI公司推出的一種針對標準TMS320調試接口的集成開發環境（IDE），利用CCS集成開發環境，用戶可以完成工程定義、程序編輯、編譯鏈接、調試和數據分析等工作環節[4]。我們把十進制的浮點數用兩個十六進制數進行表示，采用C語言實現。

再利用CCS中的File->Load Data將十六進制的數據導入到DSP的相應內存中去。

反過來，DSP處理之后的數據利用CCS的數據導出File->Save以文本文件形式保存，再用C語言進行數據逆轉化，把兩個十六進制數進行轉化成十進制的浮點數。

其中的result數組就是十進制的浮點型，origin數組就是十六進制的浮點型。

3.2核心匯編程序介紹

以下是以16位定點乘法實現32位浮點乘法的部分匯編程序：

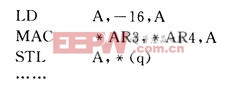
本文選用基于TI公司的TMS320C54X系列的DSP芯片開發平臺。借助DSP快速數據處理的優點，對癲癇腦電信號進行小波變換，然后濾除小尺度（高頻）成分，保留大尺寸（低頻）成分，最后再對處理后的信號進行重建。

更多醫療電子信息請關注：21ic醫療電子