無功功率計量中移相法的FPGA實現

3 Hilbert 變換計算無功功率

3.1 Hilbert 數字濾波器基本原理

理想的Hilbert 變換的定義為：

其幅值和相角分別為：

由式(6)~ 式(7) 可以看出，Hilbert 數字濾波器的幅值特性為1， 信號通過Hilbert 數字濾波器后， 其負頻率成分進行相移π/2， 正頻率成分進行相移-π/2。可見，Hilbert 數字濾波器能用于實現式(4) 計算無功功率。

3.2 FIR 型Hilbert 數字濾波器的Matlab 設計

線性相位FIR 數字濾波器的設計方法主要有窗函數法、頻率抽樣法和等波紋切比雪夫法( 即最優法) ， 本文采用等波紋切比雪夫法進行數字濾波器的設計。對于50 Hz 的工頻基波信號， 若考慮最高諧波次數為19， 則可以將該數字濾波器所關心的頻率范圍設計為40 Hz~960 Hz。根據奈奎斯特采樣定理， 采樣頻率Fs 應不小于2 倍的最高次諧波頻率， 所以至少取2 kHz。

Hilbert 數字濾波器取N 為奇數， 設所要設計的濾波器的頻率響應為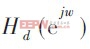， 逼近加權函數為W(w)， 用線性相位FIR 數字濾波器的H(w) 做逼近函數， 則逼近誤差函數為：

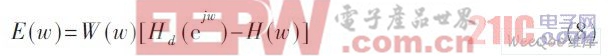
令δ=max{|E(w)|} ， 數字濾波器的設計問題就是尋找使δ最小的系統函數H(w)，即獲取最優的單位沖激響應h(n)。所以數字濾波器應有式(9)所要求的頻率響應：

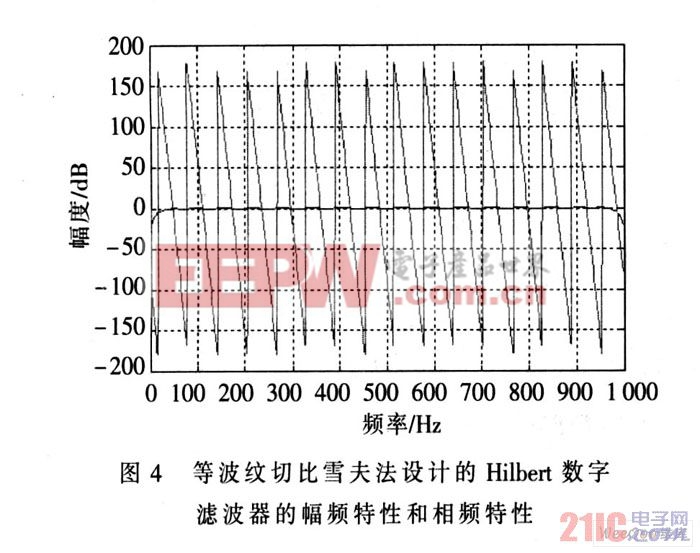
圖4 所示為等波紋切比雪夫法設計的Hilbert 數字濾波器的幅頻特性和相頻特性。從圖中可以看出該數字濾波器具有良好的幅頻特性和相頻特性， 能獲得嚴格線性相位及很好的衰減特性。