一種脫機手寫簽名認證方法

1 引言
手寫簽名認證方法屬于生物測定技術。簽名認證與其他生物測定技術相比，具有難以模仿、區分性較高、尊重隱私權、信息獲取高效等優點，在特征的可搜集性、人體傷害可接受性和魯棒性方面都很突出，具有廣闊的應用前景。但與其他生物測定方法相比，手寫簽名認證的識別率并不是很高，尤其是脫機中文手寫簽名認證。因為在脫機簽名認證中，丟失了書寫過程中的動態信息，使可利用的信息減少，增加了鑒別的難度。另外，有些高超的偽造簽名模仿得惟妙惟肖，有時即使是人類專家進行鑒定，識別率也可能會很低。這里針對脫機中文簽名，提出一種主成分特征提取和徑向基神經網絡相結合的脫機手寫簽名認證方法。

2 主成分特征提取
假設x是一個N×1的隨機向量，即x的每個元素xi都是一個隨機變量。x的均值可用L個樣本向量估計：

而其協方差矩陣可由式(2)估計：

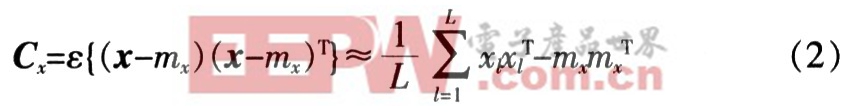
協方差矩陣是N×N的實對稱矩陣。對角元素是各個隨機變量的方差，非對角元素是它們的協方差。用矩陣A定義一個線性變換，它可由任意向量x通過式(3)得一個新向量y：

式中，A的行向量就是Cx的特征向量。
這里為了方便，對這些行向量按使得其對應的特征值遞減的順序排列。變換后的向量y是具有零均值的隨機向量，其協方差矩陣與x的協方差矩陣的關系為：

由于A的行向量是Cx的特征向量，所以Cy是對角陣且其對角元素為Cx的特征值。于是：

從而λk也是Cy的特征值。因為Cy的非對角元素都是零，所以y個元素之間都是不相關的。于是線性變換A去掉了變量間的相關性。此外，λk是第k個變換后的變量yk的方差。可通過略去對應于較小特征值的一個或多個特征向量給y降維。令B為M×N的矩陣(MN)，B是通過丟棄A的下面N-M行，并假定m=0構成的，這樣，變換向量變小(即成為M×1維)：

MSE只是與被舍棄的特征向量對應的特征值之和。通常，特征值幅度差別很大，可忽略其中一些較小值而不會引起很大誤差。