基于ADS的接收機碼元同步算法實現
加入技術交流群
假設接收信號為：
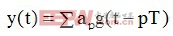，式中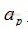
為傳輸的復數數據，
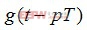為基帶成型濾波波形，對
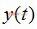的采樣值可能產生定時誤差，Gardner算法提取的定時誤差為：
（2-1）其中索引r表示符號數目，同相I和正交Q方向的第r個符號的判決值分別表示為
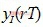和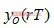
。同樣，將r和（r-1）兩個判決點中心位置的采樣值表示為
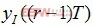和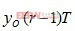
。整個誤差是I和Q兩個方向的定時誤差之和，且此誤差與載波相位無關。式中
,
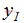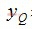表示同相和正交分量，T為符號周期。Gardner算法適用于跟蹤和捕獲模式。本文引用地址：http://www.czjhyjcfj.com/article/185592.htm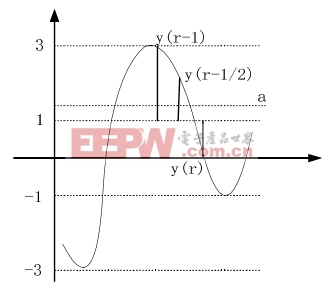
圖3 16QAM解調后波形
在 16QAM調制信號中，例如果符號從－1變為1，1變為－1，－3變為3，3變為－3等的時候，則沒有定時誤差時，中間點的平均值應為零。而有定時誤差時，將會產生一個非零的值，它的大小與差錯的大小成正比。另外一些情況，當沒有定時誤差時，中間點的平均值并不是零。例如符號從3變為－1，當沒有定時誤差時，中間點的平均值是1，如圖3所示。
如果直接把Gardner算法運用在16QAM解調系統中，定時誤差檢測的結果有些點上是正確的，有些點上是錯誤的。對于大量數據，這些錯誤的平均值是零，因為沒有定時誤差的情況，中間點可能是0，－1，1，－2，2，其平均值為零。因此這些錯誤會導致定時時鐘的抖動，通過濾波器可以減小這些抖動。
為了消除這些抖動。我們對Gardner算法做了進一步改進，其改進后算法為：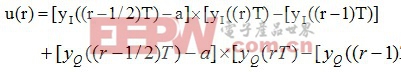
（2-2）
其中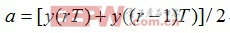
當定時超前，誤差為負，定時滯后，誤差為正。Gardner算法具有兩個特點：一是每個符號只需要兩個采樣點，且以碼元速率輸出誤差信號；二是估計算法是獨立于載波相位的，不受載波相位偏移的影響，即可以在載波相位同步之前，進行定時誤差估計。
評論