自適應濾波算法的仿真及工程實現(xiàn)
加入技術交流群
自適應濾波理論是20世紀50年代末開始發(fā)展起來的。它是現(xiàn)代信號處理技術的重要組成部分，對復雜信號的處理具有獨特的功能。自適應濾波器在信號處理中屬于隨機信號處理的范疇。對于隨機數(shù)字信號的濾波處理，通常有維納(Weiner)濾波器、卡爾曼(Kal-man)濾波器和自適應(Adaptive)濾波器。維納濾波器的權系數(shù)是固定的，適用于平穩(wěn)隨機信號；卡爾曼濾波器的權系數(shù)是可變的，適用于非平穩(wěn)隨機信號。但是，只有在對信號和噪聲的統(tǒng)計特性先驗已知的情況下，這兩種濾波器才能獲得最優(yōu)濾波。但在實際應用中，常無法確定這些統(tǒng)計特性的先驗知識，或統(tǒng)計特性是隨時間變化的，因此，在許多情況下，維納濾波器或卡爾曼濾波器實現(xiàn)不了最優(yōu)濾波，而自適應濾波不要求已知信號和噪聲的統(tǒng)計特性，因而可以提供理想的濾波性能。當前，自適應濾波技術已廣泛應用于自適應噪聲對消、語音編碼、自適應網(wǎng)絡均衡器、雷達動目標顯示、機載雷達雜波抑制、自適應天線旁瓣對消等眾多領域。
在一些信號和噪聲特性無法預知或它們是隨時間變化的情況下，自適應濾波器通過自適應濾波算法調(diào)整濾波器系數(shù)，使得濾波器的特性隨信號和噪聲的變化而變化，以達到最優(yōu)濾波的效果。這里在對自適應濾波算法研究的基礎上，給出了不同信噪比情況下，LMS算法的仿真實現(xiàn)及基于DSP的工程實現(xiàn)，并對兩種實現(xiàn)方法的結果進行了驗證、分析比較。
1 自適應濾波理論
所謂自適應濾波，就是利用前一時刻已獲得的濾波器參數(shù)等結果，自動調(diào)節(jié)現(xiàn)時刻的濾波器參數(shù)，以適應信號和噪聲未知或隨時間變化的統(tǒng)計特性，從而實現(xiàn)最優(yōu)濾波。自適應濾波器由兩個部分組成：一是濾波器的結構；二是調(diào)節(jié)濾波器系數(shù)的自適應算法。自適應濾波器的特點是自動調(diào)節(jié)自身的沖激響應，達到最優(yōu)濾波，此算法適用于平穩(wěn)和非平穩(wěn)隨機信號，并且不要求知道信號和噪聲的統(tǒng)計特性。
1．1 自適應濾波器結構
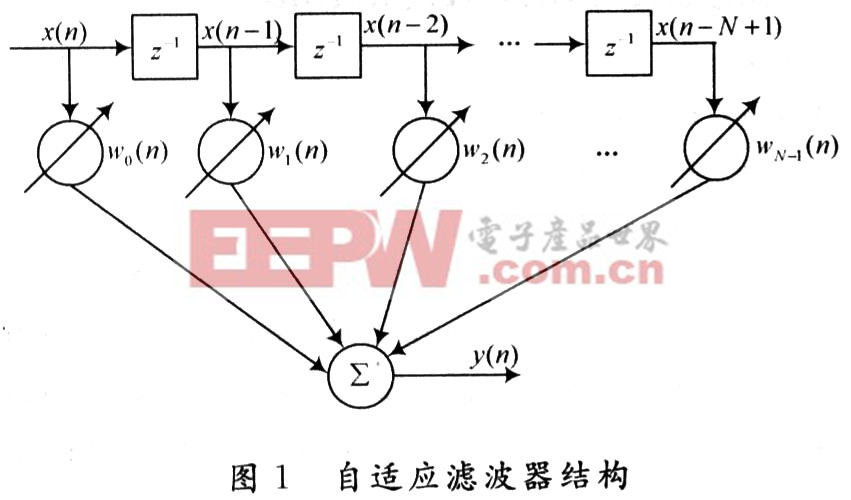
自適應濾波器主要有無限沖激響應(IIR)和有限沖激響應(FIR)兩種類型。濾波器結構的選擇對算法的處理起著重要的影響；IIR型結構濾波器的傳輸函數(shù)既有零點又有極點，它可以用不高的階數(shù)實現(xiàn)具有陡峭通帶特性，缺點是穩(wěn)定性不好，且相位特性難于控制。FIR濾波器是全零點濾波器，它是穩(wěn)定的，且能實現(xiàn)線性的相位特性，因此，自適應濾波器的結構通常采用F1R型濾波器的橫向結構，結構如圖1所示。
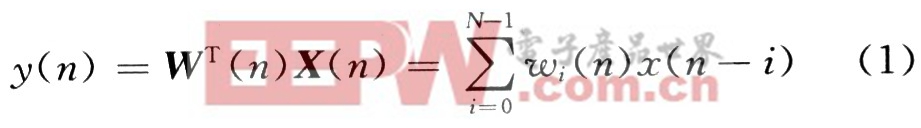
式中：n為時間序列；N為濾波器階數(shù)；x(n)=[x(n)，x(n-1)，…，x(n-N+1)]T為輸入矢量；W(n)=[ω0(n)，ω1(n)，…，ωN-1(n)]T為權系數(shù)矢量。
1．2 LMS自適應濾波算法
LMS自適應濾波算法是根據(jù)最小均方誤差準則進行設計的，LMS算法的目的是通過調(diào)整系數(shù)，使輸出誤差序列的均方值最小化，并且根據(jù)這個數(shù)據(jù)來修改權系數(shù)。誤差序列的均方值ε表示為：
式中：d(n)為理想信號；e(n)為輸出誤差序列。將式(1)中的y(n)代人式(2)中有：
式中：R=E[X(n)XT(n)]為N×N自相關矩陣，表示輸入信號采樣值間的相關性矩陣。P=E[d(n)X(n)]為N×1互相關矩陣，表示理想信號d(n)與輸入信號矢量的相關性。
在均方誤差最小時，最佳權系數(shù)
應滿足如下方程：
即：
這是一個線性方程組，如果R矩陣為滿秩矩陣，則有R-1存在，可得到權系數(shù)的最佳值滿足：
由式(6)可以知道，求出R和P就可以得到W*。由前幾式可知，R是X(n)的自相關矩陣，P是d(n)與 X(n)的互相關矢量。
LMS算法是以最陡下降法為原則的迭代算法，即W(n+1)矢量是W(n)矢量按均方誤差性能平面的復斜率大小調(diào)節(jié)響應一個增量，即：
式中：u表示自適應步長；
(n)為n次迭代的梯度，表示為：
由式(7)產(chǎn)生了求解最佳權系數(shù)W*方法的兩種方法，一種是最陡梯度法，其基本思路為：設定初始權系數(shù)W(0)，用式(7)迭代公式計算，迭代直到W(n+1)與 W(n)誤差小于規(guī)定范圍。其中(n)的E[]計算可用下面的估計值表達式來計算：
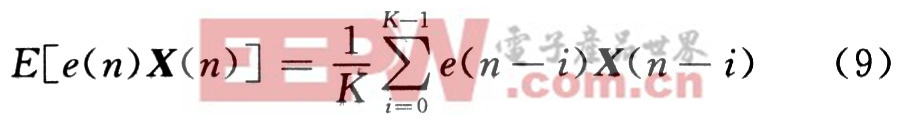
式中K取值應足夠大。如果用瞬時-2e(n)X(n)來代替上面對-2E[e(n)X(n)]的估計運算，就產(chǎn)生另一種算法：隨機梯度法，即Widrow-Hoff的LMS算法。迭代公式表示為：
評論