Hopfield網絡求解TSP兩種改進算法的仿真研究
首先檢查式(1)的前3項,其中,第3項僅在網絡輸出全為0時起約束作用,否則前2項已保證第3項成立。對前2項作如下修改:
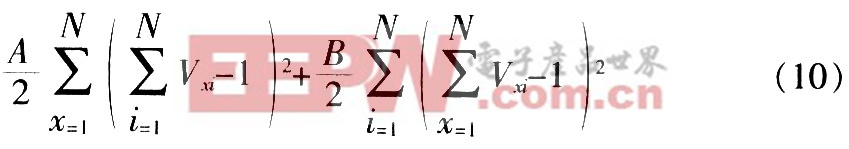
則第3項完全可省去。將優化目標項寫成:本文引用地址:http://www.czjhyjcfj.com/article/163388.htm
或
也可滿足優化要求。則TSP的能量函數簡化為:

下面以式(13)作為研究對象,其對應的網絡連接矩陣和外部輸入分別是:

該算法可從理論上證明其有效性,仿真研究如下:取A=B=3,D=1,步長δt=0.05,對Uo=0.02和軟限幅兩種情況進行仿真,仿真終止條件與改進算法2相同。測試的統計結果如表2和圖2所示。
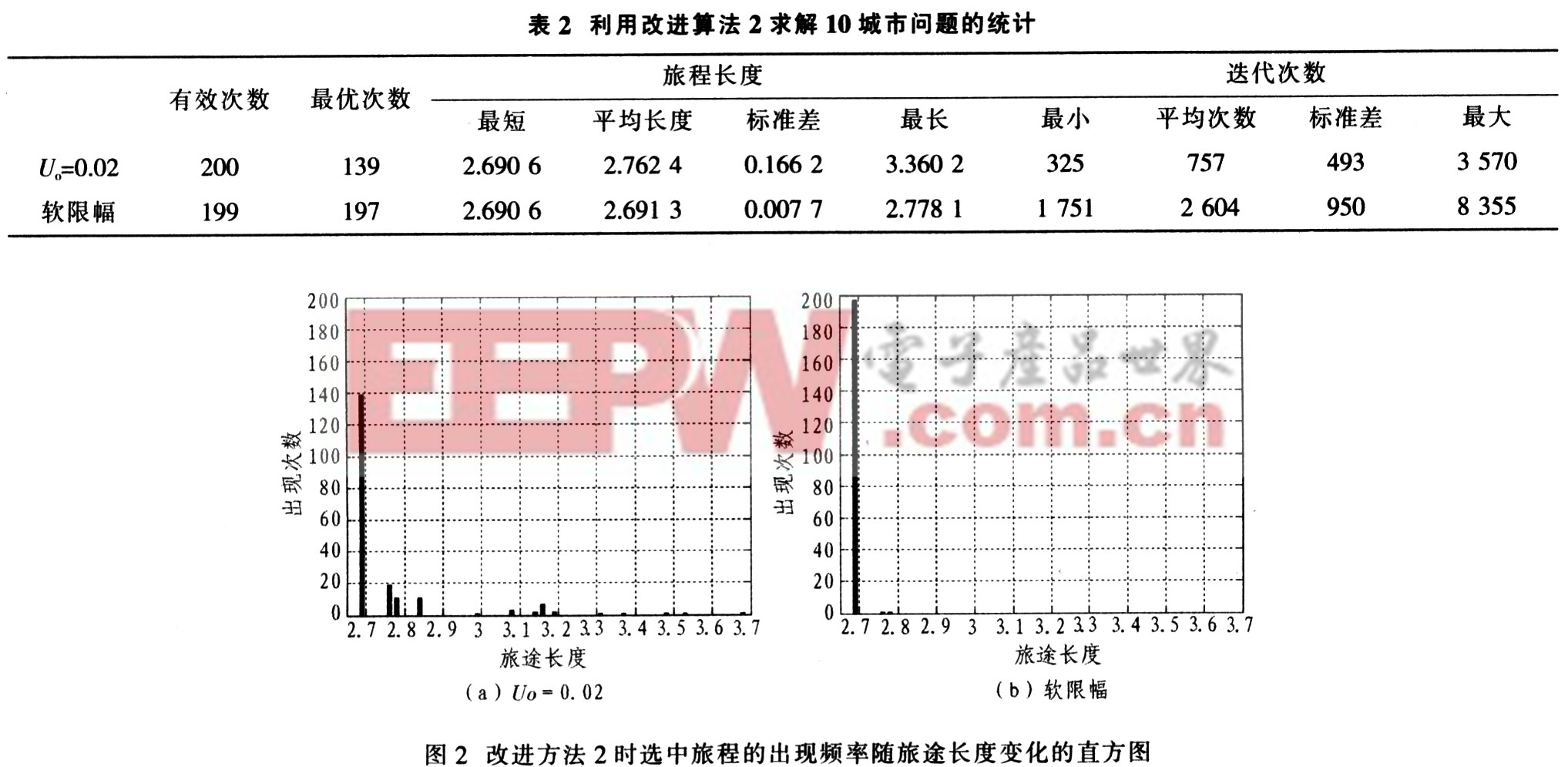
從測試結果可以看出,該方法獲得的最優解的個數明顯的多于改進算法1。軟限幅的效果明顯優于sigmold函數的效果。但所需的收斂次數較多。這一點與改進算法1是一致的。在使用軟限幅時獲得最優解的概率大于95%,只是所需迭代次數稍多。
4 結束語
對兩種求解TSP的改進算法進行仿真研究,結果表明他們具有非常好的優化效果,在10城市問題上可近似100%的獲得最優解。
另外,該算法還具有對參數敏感度低的優點。改進算法的缺點是所需迭代次數較多。當采用大步長迭代時,可降低收斂所需的迭代次數,但會影響優化效果。
這種影響對Uo=0.02的情況不明顯,例如,在δt=0.5時,其優化效果與δt=0.05時幾乎相同,所需迭代次數可降到450次左右。而對于軟限幅的情況,步長的影響就明顯了,δt= 0.5時,優化效果與圖中Uo=0.02的情況差不多。下一步的工作擬采用變步長的方法,估計可大大降低所需的迭代次數。






評論