渦街流量計的工作原理及應用

　在特定的流動條件下，一部分流體動能會轉化為流體振動，其振動頻率與流速(流量)有確定的比例關系，依據這種原理工作的流量計稱為流體振動流量計。目前流體振動流量計有三類：渦街流量計、旋進(旋渦進動)流量計和射流流量計。渦街流量計具有以下一些特點：

　　①輸出為脈沖頻率，其頻率與被測流體的實際體積流量成正比，不受流體組分、密度、壓力、溫度的影響;

　　②測量范圍寬，一般范圍度可達10：1以上;

　　③精確度為中上水平;

　　④無可動部件，可靠性高;

　　⑤結構簡單牢固，安裝方便，維護費較低;

　　⑥應用范圍廣泛，可適用液體、氣體和蒸汽。

　　渦街流量計的工作原理

　　在流體中設置旋渦發生體(阻流體)，從旋渦發生體兩側交替地產生有規則的旋渦，這種旋渦稱為卡曼渦街(見圖1)，旋渦列在旋渦發生體下游非對稱地排列。根據卡曼渦街原理，有如下關系式：

(1)

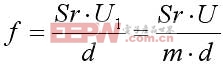
(2)

　　式中，m為旋渦發生體兩側弓形面積與管道橫截面面積之比;D為表體通徑;d為旋渦發生體迎面寬度;f為旋渦的發生頻率;U1為旋渦發生體兩側平均流速;Sr為斯特勞哈爾數;U為被測介質流的平均速度。

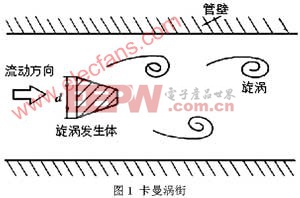
　　圖1 卡曼渦街

　　管道內體積流量qv為：

(3)

(4)

　　式中， K為流量計的儀表系數，單位為脈沖數/m3。

　　K除與旋渦發生體、管道的幾何尺寸有關外，還與斯特勞哈爾數有關。斯特勞哈爾數為無量綱參數，它與旋渦發生體形狀及雷諾數有關，圖2為圓柱 狀旋渦發生體的斯特勞哈爾數與管道雷諾數的關系圖。由圖2可見，在ReD=2×104～7×106的范圍內，Sr可視為常數，這是儀表正常工作范圍。當測 量氣體流量時，渦街流量計的流量計算式為

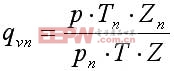
(5)

　　式中，qVn、qV分別為標準狀態下(0℃或20℃，101.325kPa)和工況下的體積流量; Pn、P分別為標準狀態下和工況下的絕對壓力;Tn、T分別為標準狀態下和工況下的熱力學溫度;Zn、Z分別為標準狀態下和工況下氣體壓縮系數。

　　圖2 斯特勞哈爾數與雷諾數關系曲線