IDMA通信系統中的粒子群交織算法

2 IDMA通信系統中的檢測原理與方法
圖1為IDMA通信系統發送和接收部分的結構圖。該系統發送端包括K個用戶，第k個用戶發送的碼元序列為：dk=[dk(1)，…，dk(i)，…，dk(I)](I為發送序列碼元長度)，經碼長為S的重復編碼擴頻得到序列為：Gk=[Gk(1)，…，Gk(j)，…，Gk(J)]，J為擴頻后的碼長，再經交織器打亂順序重排后成為發送序列為：Xk=[xk(1)，…，xk(j)，…xk(J)]。

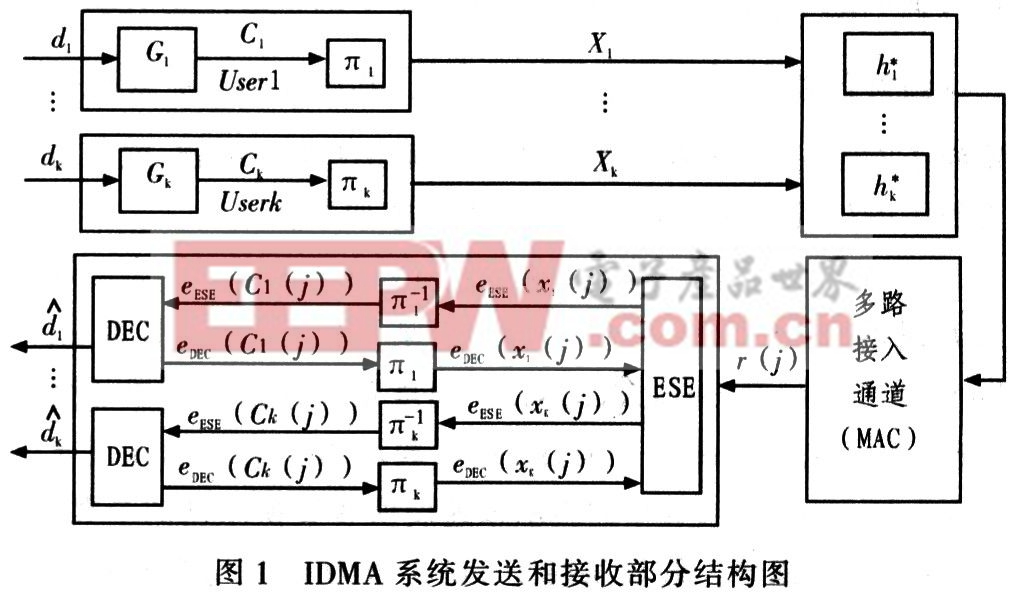
系統接收端采用Turbo型迭代譯碼結構，主要由基本信號檢測器ESE、解交織器和K個用戶譯碼器DEC組成。系統中考慮完全同步無記憶信道，接收信號r(j)表示為：

式中，n(j)為高斯白噪聲采樣，hk為第k個用戶的信道衰落系數，ζk(k)為第后個用戶第j個碼片的失真，根據中心極限定理，ζk(j)滿足近似高斯分布，可用均值和方差函數表示。
基本信號檢測器模塊ESE的檢測算法概括如下：

式中E(．)表示均值，V(．)表示方差。
譯碼器DEC反饋的先驗信息經交織后得到eDEC[xk(j)]，更新ESE中接收信號的均值和方差，并產生輸入到譯碼器DEC的外信息eESE(xk(j))，外信息經過解交織，作為譯碼器DEC輸入端的先驗信息，如此循環迭代直到規定的次數以后，K個用戶的譯碼器分別產生相應信息序列的硬判決值dk。

3 基于粒子群的交織算法
3．1 粒子群算法的相關定義與操作
粒子群算法是一種基于迭代的優化方法，具有易于實現、需要調整的參數少等優點，并且在較少的迭代次數的情況下就可獲得全局最優解。設粒子群粒子個數為M，在一個D維的搜索空間中，粒子i(1≤i≤M)在第k次迭代時的位置信息為速度信息表示為搜索空間的任意數，即粒子到目前為止所經歷的最好位置為群體中所有粒子到目前為止所經歷過的最好位置為其中b為具有最優位置粒子的索引。為使粒子群算法能正確解決交織問題，這里定義粒子的位置和速度的含義及相關操作如下：
(1)粒子定義粒子的位置定義為一序列。對于搜索空間為D維的種群，序列長度為D。假設某個粒子j的位置為xj，D=5，則可表示為xj=(1，2，3，4，5)；速度定義為粒子位置的變換集，即一組置換序列的有序列表，表示為：v={(ik,jk)，ik,jk∈D}，k∈{1，2，…，|v|，其中|v|表示該速度所含置換序列的個數。
(2)置換操作 假設某粒子i的位置為xi，定義置換序列(mi,ni)，置換操作用以交換xi中第mi和ni個值的位置，則x'i=xi+(mi,ni)，其中x'i為經過置換操作后得到的新位置。
(3)加法操作包括粒子速度與速度的加法操作及粒子速度和位置的加法操作。設vi、vj、vk分別表示第i、第j及第k個粒子速度，xk為第k個粒子位置。vi+vj表示兩個速度相加的操作，其結果為兩個置換序列合并，產生一個新置換序列串；vk+xk表示速度和位置的加法操作，即將一組置換序列依次作用于某個粒子位置。其結果為一個新位置。
(4)減法操作主要指粒子位置與位置的減法操作。該操作相減后結果為一組置換序列，即速度。設xk為第k個粒子位置，xi為第i個粒子位置，則xi-xk為一個置換序列。例如：xi=(1，2，3，4，5)，xk=(2，3，1，4，5)，由于xi(1)=1，xk(3)=1，第1個交換序列為(1，3)，xj=xk(1，3)=(1，3，2，4，5)；又xi(2)=2，xi(3)=2，第2個交換序列為(2，3)，xi=xj+(2，3)，因此經上述操作得到：xi=xk+{(1，3)，(2，3)}，所以xi-xk={(1，3)，(2，3)}。
(5)乘法操作 指實數與粒子速度的乘法操作。對于在(0，1)任意實數c，設速度v有i個置換序列，則乘法操作截取速度置換序列，使新的速度置換序列個數為|cxi|(cxi取整)。
根據以上定義，粒子群的更新公式可描述為：

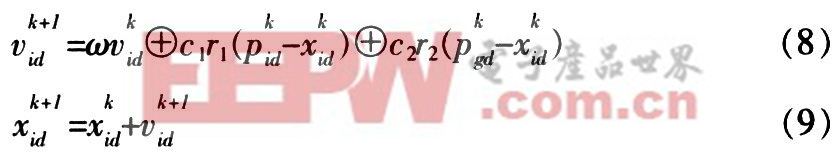
式中，c1與c2是兩個正的常數，稱為加速因子，r1和r2為分布于[0，1]間的隨機數。
3．2 粒子群交織算法
對于碼片長度為J的序列，其交織方式有J!種。當J較小，而用戶數較大時，隨機產生的交織序列之間的互相關系數接近1，交織區分用戶時，嚴重影響兩個用戶間通信的性能。粒子群算法能搜索到全局最優解，可選擇互相關性最弱的交織序列區分用戶，從而提高通信性能。
在數據傳輸中，碼片長度J=IxS，其中I為傳輸序列碼元長度。S為擴頻碼長度。粒子群交織是從J!個交織序列中選擇K個互相關性弱的序列區分用戶，但J!個解在實際操作中運算量較大，故選擇N個作為初始解。粒子群交織算法中選擇互相關矩陣作為適應度函數。X為N×J的數據矩陣，是N個可能的解，每個解是長度為J的交織序列，其元素為X(n,J)∈｛－1，1}(n=1，…，N，j=1，…，J)；INDEX表示一個，N×J的矩陣，其值是對應數據矩陣X的交織序列的索引值；R是X的互相關系數矩陣，為N×N維，R的元素R(i，j)由下式計算得到：

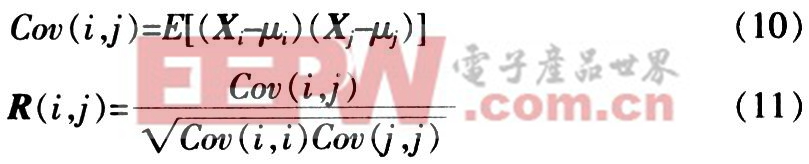
式中，Xi是矩陣X的第i行向量，μi=E(Xi)，E表示數學期望。