基于FPGA的高速定點FFT算法的設計方案

引 言
快速傅里葉變換(FFT)作為計算和分析工具，在眾多學科領域(如信號處理、圖像處理、生物信息學、計算物理、應用數學等)有著廣泛的應用。在高速數字信號處理領域，如雷達信號處理，FFT的處理速度往往是整個系統設計性能的關鍵所在。
針對高速實時信號處理的要求，軟件實現方法顯然滿足不了其需要。近年來現場可編程門陣列(FPGA)以其高性能、高靈活性、友好的開發環境、在線可編程等特點，使得基于FPGA的設計可以滿足實時數字信號處理的要求，在市場競爭中具有很大的優勢。
在FFT算法中，數據的寬度通常都是固定的寬度。然而，在FFT的運算過程中，特別是乘法運算中，運算的結果將不可避免地帶來誤差。因此，為了保證結果的準確性，采用定點分析是非常必要的。

1 FFT算法原理
FFT算法的基本思想就是利用權函數的周期性、對稱性、特殊性及周期N的可互換性，將較長序列的DFT運算逐次分解為較短序列的DFT運算。針對N=2的整數次冪，FFT算法有基-2算法、基-4算法、實因子算法和分裂基算法等。這里，從處理速度和占用資源的角度考慮，選用基-4按時間抽取FFT算法 (DIT)。對于N=4γ，基-4 DIT具有log4N=γ次迭代運算，每次迭代包含N／4個蝶形單元。蝶形單元的運算表達式為：

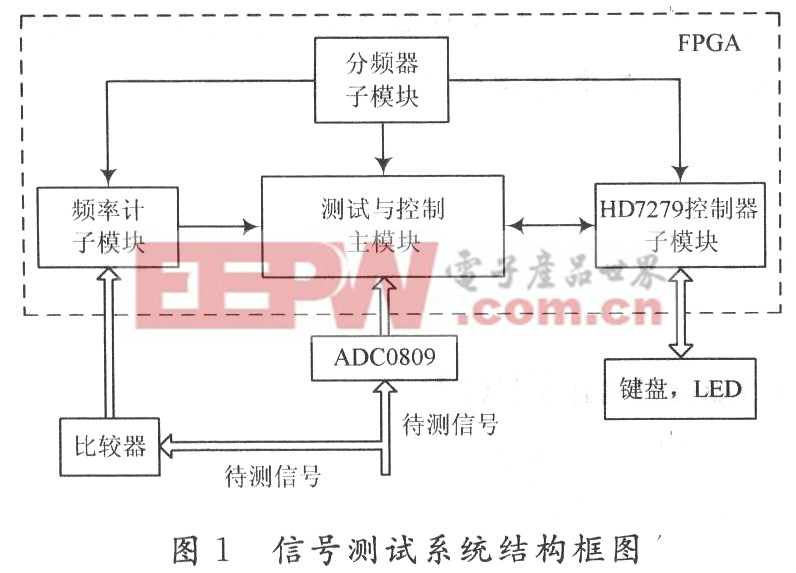
其信號流如圖1。式中：A，B，C，D和A′，B′，C′，D′均為復數據；W=e-j2π/N。進行1次蝶形運算共需3次復乘和8次復加運算。N=64 點的基-4DIT信號流其輸入數據序列是按自然順序排列的，輸出結果需經過整序。64點數據只需進行3次迭代運算，每次迭代運算含有N／4=16個蝶形單元。

2 FFT算法的硬件實現
2．1 流水線方式FFT算法的實現
為了提高FFT工作頻率和節省FPGA資源，采用3級流水線結構實現64點的FFT運算。流水線處理器的結構如圖2所示。

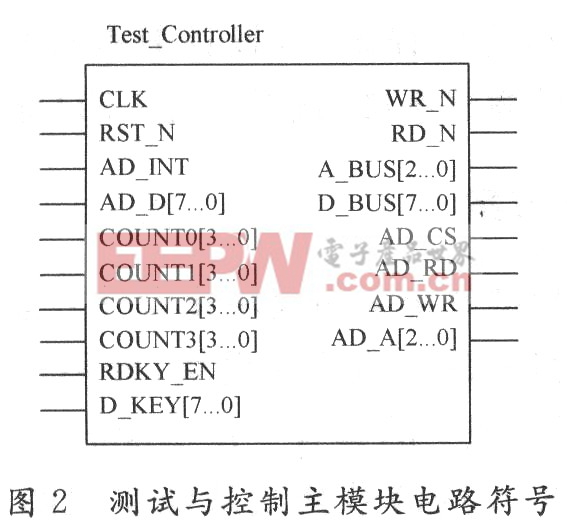
每級均由延時單元、轉接器(SW)、蝶形運算和旋轉因子乘法4個模塊組成，延時節拍由方框中的數字表示。各級轉接器和延時單元起到對序列進行碼位抽取并將數據拉齊的作用。每級延時在FPGA內部用FIFO實現，不需要對序列進行尋址即可實現延時功能。數據串行輸入，經過3級流水處理后，串行輸出。