整周模糊度的快速求解算法
1.1 備選整周模糊度解集的確定
利用GPS雙差載波相位測量時,其數學模型為: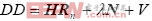

P0/0、X0/0初值的選取取決于對基線向量和初始模糊度范圍的了解,基線分量及其變化速度分量初值可取為零,方差初值根據載體的動態情況選擇,整周模糊度分量初值可取為偽距雙差觀測值,方差初值根據偽距的測量精度選擇。
如果系統動態模型建立得比較準確(如靜態時或載體運動規律已知時),則當卡爾曼濾波器穩定后,整周模糊度估計值一般具有較高的精度,可以直接取與其最接近的整數作為整周模糊度,但一般需要較長的時間才能得到正確的模糊度,對于實時性要求較高的場合不適用。實際應用時一般是當Kalman濾波達到一定



圖1 整數高斯變換前的置信橢圓 圖2 整數高斯變換后的置信橢圓
為進一步減少備選整周模糊度組合,將所有的使用衛星分為兩組:選4顆衛星作為主組,用來確定模糊度的搜索空間,其余衛星作為從組,用于模糊度的檢驗。
對選為主組的4顆衛星,取其雙差模糊度的浮點估計值及其方差陣進行高斯變換,得變換后的模糊度估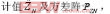 ,將對主組雙差模糊度按式(16)確定的置信空間中的所有組合作為備選整周模糊度解集。
,將對主組雙差模糊度按式(16)確定的置信空間中的所有組合作為備選整周模糊度解集。






評論