「技術文章」使用有效位數（ENOB）對ADC建模

了解ADC的ENOB（有效位數）的概念，以及如何將其用于系統仿真中的數據轉換器建模。

在本系列關于數據轉換器建模的上一篇文章中，我們討論了ADC模型提出了如何選擇一個輸入信號來實現一個模型。（請注意，這篇初始文章包括一個重要的縮略語、詞匯表和參考文獻。）

在這里，我們將繼續討論這個話題，討論數據轉換器常用的一個優點，即“有效位數”或ENOB（[4]到[8]）。

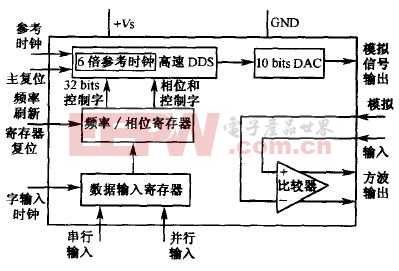
ENOB被定義為一個理想量化器在相同條件下必須執行與數據轉換器相同的比特數。可以使用圖1中顯示的模型，其中NE= ENOB.

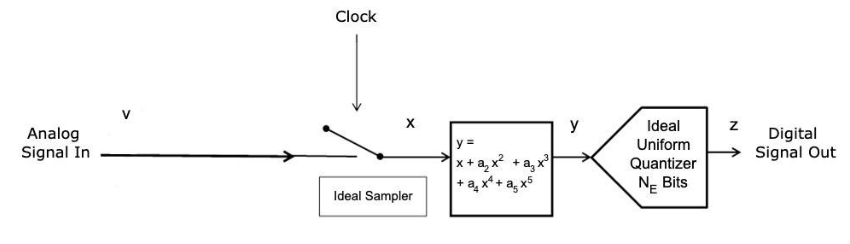
圖1ADC模型

問題出現了：“這些條件是什么？它們對應用程序的使用是否相同？ENOB是否有不同的定義，應用于不同的應用？

通常ENOB定義為給定頻率的0 dBpeakFS正弦波輸入[8]。它通常是頻率的函數。設LSB電壓為L，理想的ADC有N位。

回到圖2，正弦波的峰值在FS處+= L((2N/2)-1) and FS- = ?L(2N/2).

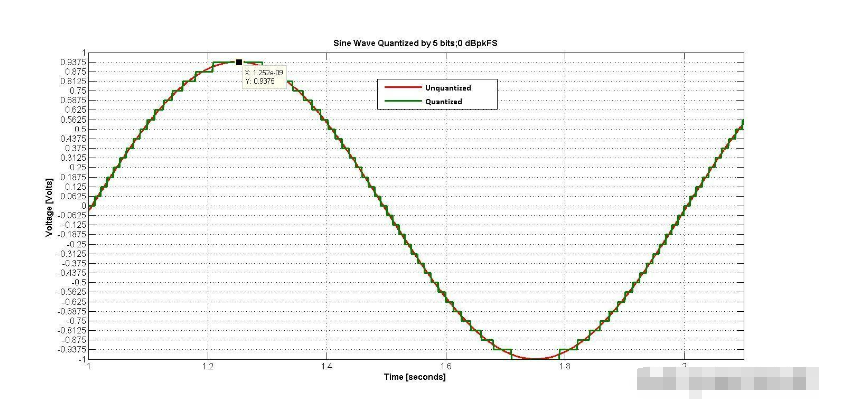
圖2上一篇文章中的圖2應如何為系統仿真建模數據轉換器

對于N≥5；假設L（（2）的誤差N/2)-1) = L(2N/2） 不到7%，所以我們開始吧。如果正弦波的峰值是L（2N/2） 其均方（ms）值為L2（22號/8). 眾所周知，對于理想ADC的隨機輸入，均方（ms）量化噪聲＝l2/12（[2]，方程1.14）；這是整個奈奎斯特區的噪聲（0到F奈奎斯特). 但是我們有一個正弦波，不是隨機輸入。您的作者想知道，對于正弦波以及ADC可能看到的其他輸入，相同的量化噪聲是否有效，所以做了一些簡單的模擬。

結果見表1

表1。差分波形量化誤差均方進入量化器，無時間采樣

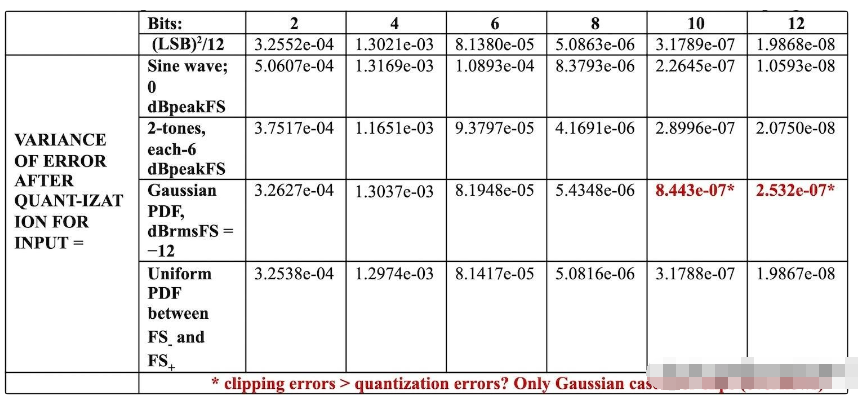
對于2到12位，使用公式L2/12顯示均方噪聲；并將其與在各種輸入下觀察到的均方噪聲進行比較。即使是單個正弦波，結果也相當接近。唯一的不一致之處是高斯輸入，在-12 dBrmsFS，對于10和12位；其中由于單獨量化而產生的噪聲將很低。然而，高斯噪聲的峰值會導致削波（過載），從而增加噪聲。

{作為一個有趣的，除了在本文件的.02版中添加的內容外，由Grey[18A]導出了0 dBpeakFS正弦輸入下的量化噪聲均方值的精確表達式：

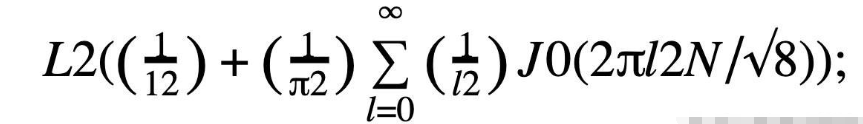
其中J0是0階的普通貝塞爾函數。對于大x，J0（x） →0；它是L2/12.}

所以，信噪比

SNR=ms（信號）/ms（噪聲）=（1.5）（22N）

或者，單位：dB

SNRdB= 6.0206N + 1.7609

對一個由取樣器和一個理想的N位量化器組成的ADC進行了模擬，結果如表2所示。輸入正弦與ADC時鐘不同步。結果與方程1非常接近。

表2。由方程1和通過模擬ADC正弦波計算的信噪比

對于實際的ADC，整個奈奎斯特區的信噪比和失真比（SINAD）被替換為等式1中的SNR，結果被解為N，現在稱為有效位數=NE。

NE= (SINADdB- 1.7609)/ 6.0206 ≈ (SINADdB- 1.76)/ 6.02

包括非線性失真在內的所有項。對于小于滿標度的輸入，ADC的失真減小。制造商通常會在某些輸入電平上測量SINAD–B dBpeakFS（峰值信號低于滿標度B dB）。由于測試輸入信號降低了B dB，因此他們會將該值相加以計算ENOB，就好像對于較大的輸入而言失真不會增加一樣。

NE= (B + SINADdB- 1.76)/ 6.02

然而，這個公式是假的，因為它忽略了失真會增加的事實，通常比信號快。對于簡單的三階非線性，信號每增加1db，失真度增加3db，因此SINAD將惡化2db。

因為互調是如此的重要，并遵循我們的“選擇一個輸入信號來實現一個模型”一節的建議上一篇文章：應使用2音輸入信號。

還需要探索“測量整個奈奎斯特帶寬”和“測量噪聲”之間的差異。圖3顯示了2音測試信號。

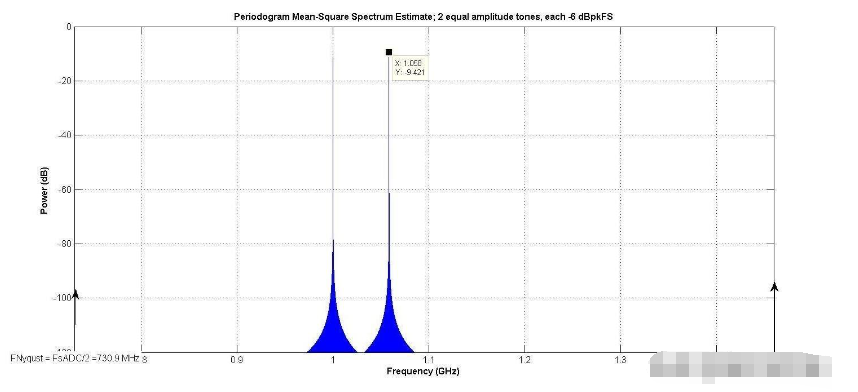
圖3

從f開始S= 1461.8 MHz, f奈奎斯特= 730.90 MHz. 信號在第二奈奎斯特區。注意，ADC的輸入可以分為奈奎斯特區。由于ADC輸出是時間采樣的，因此第一奈奎斯特區以上的頻率不存在，所以這就是奈奎斯特區。

還使用了1000兆赫的1階測試信號。“有趣的音調”的中心頻率是233.7兆赫。對圖1的模型進行了模擬E是理想量化器的位數

圖4顯示了2音調測試的輸出，模擬了一個8位ADC。由于沒有明顯的雜音（雜散），因此1音和2音輸入情況下的SINAD等于SNR。

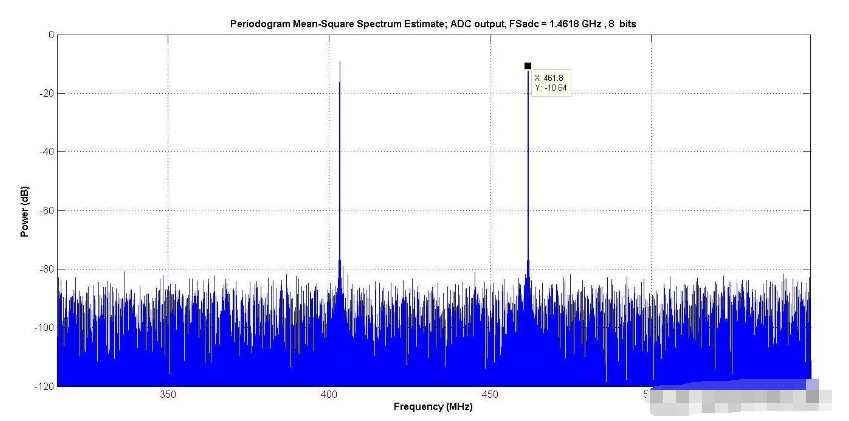
圖4

當我們繪制由位函數確定的SINAD時，有兩個觀測值。

首先，奈奎斯特帶寬和“感興趣帶寬”之間的差異是3.1275；相當于4.95 dB。因為這近似于奈奎斯特帶寬曲線與相同輸入的“感興趣帶寬”曲線之間的差異；這與量化噪聲頻譜為白色的假設一致。

其次，為了使峰值達到0 dBpeakFS，雙階情況的平均功率必須是單階情況的?。相同帶寬的1階和2階曲線之間的差值約為3 dB。

對于單階輸入，它也與等式2很好地匹配。可以定義兩個不同的ENOB，將測量的SINAD與ENOB1和ENOB2輸入

ENOB1≡ (SINADN1- 1.76)/6.02

ENOB2≡ (SINADN2+1.25)/6.02

SINADNi是測量的SINAD，單位為dB，用于整個奈奎斯特帶寬，用于輸入階。對于圖1的模型，兩個ENOB是相等的。

本系列的下一篇文章將討論另一個模型，它使用互調多項式和有效比特數。