- 什么是傅里葉變換傅里葉變換(Transformée de Fourier)是一種積分變換。因其基本思想首先由法國學者傅里葉 ...
- 關鍵字:
傅里葉變換 運算 微分方程
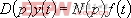
- 一、 線性系統微分方程線性的證明 線性系統必須同時滿足齊次性與疊加性。所以,要證明線性系統的微分方程是否是線性的,
- 關鍵字:
系統 響應 微分方程
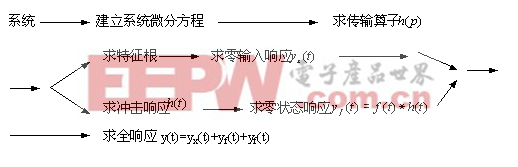
- 不涉及任何數學變換,而直接在時間變量域內對系統進行分析,稱為系統的時域分析。其方法有兩種:時域經典法與時域卷積法。 時域經典法就是直接求解系統微分方程的方
- 關鍵字:
傳輸 算子 微分方程 模型 數學 系統
微分方程介紹
您好,目前還沒有人創建詞條微分方程!
歡迎您創建該詞條,闡述對微分方程的理解,并與今后在此搜索微分方程的朋友們分享。
創建詞條
關于我們 -
廣告服務 -
企業會員服務 -
網站地圖 -
聯系我們 -
征稿 -
友情鏈接 -
手機EEPW
Copyright ?2000-2015 ELECTRONIC ENGINEERING & PRODUCT WORLD. All rights reserved.
《電子產品世界》雜志社 版權所有 北京東曉國際技術信息咨詢有限公司

京ICP備12027778號-2 北京市公安局備案:1101082052 京公網安備11010802012473