基于稀疏信號結構信息的壓縮檢測算法
為了進一步驗證算法的有效性,下面針對應用于雷達系統中的線性調頻信號進行檢測。在雷達系統中,線性調頻信號是一種非常重要的信號形式,信號瞬時頻帶寬的特性雖然提高了雷達系統的目標檢測及識別能力,卻給信號采集及數據處理帶來極大壓力,如何使用較少的采集數據完成檢測是一個關鍵技術[7]。在這里,我們使用文獻[12]中的四參量chirplet字典來生成線性調頻信號。設生成的線性調頻信號的信號長度為1024,相對chirplet字典的稀疏系數滿足正態分布[4],這里稀疏度設為5,信噪比為10dB。下面驗證本文所提算法與MP檢測算法在不同測量點數下的對線性調頻信號的檢測性能。
本文引用地址:http://www.czjhyjcfj.com/article/203220.htm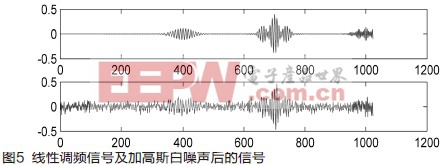
從圖中可以看出,本文所提算法能使用較少的測量點數獲得較高的檢測性能,這可以減輕接收系統系統在采樣和數據處理方面的壓力。
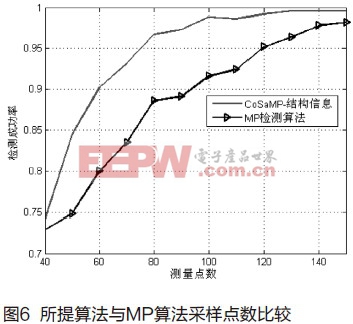
結束語
本文基于稀疏信號的結構信息提出一種新的壓縮檢測方法,該方法利用改進的壓縮采樣匹配追蹤(CoSaMP)部分重構算法獲得目標信號的估計,通過對比位置與幅值信息的相似度來完成檢測。與原有的檢測方法相比,本文提出的方法更高效、更快速、更穩定。實驗結果表明,在低信噪比時,本文方法在較少的迭代次數下,可以使用較少的采樣數據獲得較高的檢測成功率。
參考文獻:
[1] E. Candès, J. Romberg, and T. Tao, Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J], IEEE Trans. Inf. Theory. 2006 , 52(2) :489–509.
[2] D. Donoho, Compressed sensing[J], IEEE Transaction on Information Theory, 2006, 52(4): 1289-1306.
[3] Y. Tsaig, D. L. Donoho, Extensions of compressed sensing[J], Signal Processing. 2006, 86(3): 549–571.
[4] M.F. Duarte, M.A. Davenport, M.B. Wakin, R.G. Baraniuk, Sparse signal detection from incoherent projection[C], IEEE Int. Conf. Acoustics Speech and Signal Processing(ICASSP), Toulouse , France, May 2006, 305-308.
[5] Jun Wu, Naian Liu, Yanfei Zhang, Changlin Shen. Blind detection of frequency hopping signals based on compressive sensing[C]. Consumer Electronic, Communication and Networks (CECNet) ,2012, 1691-1694.
[6] J. Haupt, R. Nowak, A. Yeh, Compressive sampling for signal classification[C], In 2006 Asilomar Conf. on Signals, System & Computer, Oct. 2006, 1430-1434.
[7] 劉冰,付平,孟升衛.基于正交匹配追蹤的壓縮感知信號檢測算法[J].儀器儀表學報,2009,31,(9):1959-1964
[8] J. Haupt, R. Nowak. Compressed sampling for signal detection [C]. IEEE Int. Conf. on Acoustics, Speech, and Signal Processing (ICASSP), Honolulu, Hawaii April 2007, 1509-1512
[9] 劉冰,付平,孟升衛.基于采樣值數字特征的壓縮感知信號檢測算法[J].儀器儀表學報,2011,32,(3):577-582
[10] Joachim H.G. Ender, On compressive sensing applied to radar [J], Signal Processing. 2010, 90(5):1402–1414.
[11] D. Needell and J.A. Tropp. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples[J],Applied and Computational Harmonic Analysis, 2009, 26(3):301–321.
[12] O. Yeste-Ojeda, J. Grajal, and G. Lopez-Risueno. Atomic decompositionfor Radar applications[J], IEEE Trans. Aerosp. Electron. Syst., 2008, 44(1): 187–200.







評論