具有較大圍長的正則LDPC碼構造方法介紹

1962年Gallager提出低密度校驗(Low DensityParity Check，LDPC)碼，后來Tanner對它進行了很有價值的補充，直到1995年又被Mackey重新提出。如果采用和積迭代譯碼算法，LDPC碼具有非常接近香農限的性能。如果在LDPC碼的Tanner圖中存在環，在迭代譯碼的過程中錯誤信息將會膨脹，對于LDPC的譯碼性能相當有害，尤其是較短環的存在，所產生的危害尤為嚴重。所以，在構造LDPC的過程當中，要盡量避免短環的出現。為了盡量減小Tanner圖中環的存在對相應LDPC碼在和積譯碼算法下所得性能的影響，一些研究學者基于代數方法和啟發式搜索方法，提出了一些具有較大圍長的LDPC碼構造方法。研究表明，通過增大LDPC碼的圍長，在一定程度上可以改善碼的糾錯性能。本文構造了正則LDPC碼，在構造過程中討論了設計圍長的參數選舉，使得滿足一定的條件就可以避免校驗矩陣的小圍長出現，使得所構造的矩陣具有較大圍長。

1．LDPC碼的構造理論

考慮長為16的(2，4)正則LDPC碼對應的Tanner，如圖1所示。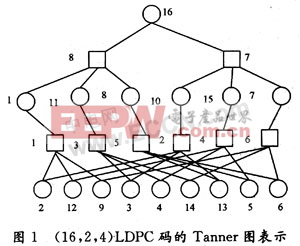


從圖1中很顯然可以看出，該Tanner中環的最小長度為8，因此對應LDPC碼的圍長也為8。

按圖1將其中的變量結點和校驗結點依次編號，可以得到對應LDPC碼的校驗矩陣，如圖2所示。


圖2矩陣很有規律，可以看作是由兩個行重為2、維數為8×8的循環方陣拼接而成。因此可以猜想，采用某些有規律的矩陣合并成校驗矩陣，這樣生成的LDPC碼很可能會具有較大的圍長。或者說，將LDPC碼的校驗矩陣分裂為若干個子矩陣，然后每個子矩陣再按照某種規律構造，就有可能避免小環的出現。

這里采用矩陣分裂的思想。設要構造一個長為72(n=ρUU∈N)的(λ，ρ)正則LDPC碼，將該碼的校驗矩陣分裂為(λ，ρ)個U×U的子矩陣。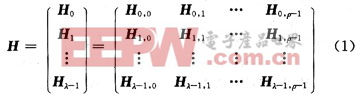



式中：每個子矩陣Hi,j=I(ai,j)(0≤iλ，0≤jρ)均為一個單位陣或者單位陣的循環移位ai,j表示該單位陣的各行循環右移的位數。顯然，這樣構造的校驗矩陣也不可能為滿秩，至多為λρ-λ-1。
為便于描述，用A=(ai,j)表示由各個子方陣的循環移位參數組成的矩陣，用(I，J，i，j)表示校驗矩陣中的元素，其中(I，J)為該元素所屬的子矩陣的坐標，(i，j)為該元素在它所屬的子矩陣中的坐標。稱Tanner圖中每個變量結點參與的所有環的最小長度為該變量結點的環長，則顯然相應LDPC碼的圍長就等于各個變量結點環長的最小值。將n個變量結點分為P組，每一組變量結點對應一列子矩陣，則考慮到各個子矩陣的循環特性，有如下定理成立。

定理1 屬于同組的變量結點具有相同的環長。

證明：設任意兩個同組的變量結點x和y，分別對應一列子矩陣的第x列和第y列，且y-x=dmodU，其環長分別為C(x)和C(y)，并設變量結點x的最小環路徑如圖3所示。



根據各個子矩陣的循環特性，可以找到另一個環的路徑如圖4所示。



顯然該環路長度為C(x)且經過變量節點y，故有：

C(x)≥C(y) (2)
同理可得：
C(x)≤C(y) (3)

綜合上面兩式，有C(x)=C(y)即對任意兩個同組的變量節點，它們的環長均相等，證畢。

由定理1可知，按照上述方法構造的校驗矩陣所對應的LDPC碼，所有變量節點的環長至多有ρ種情況，因此對這樣構造的矩陣只需要分別從各組中抽取一個變量節點，然后只對這ρ個變量節點進行檢測，即可確定整個碼的圍長。

2校驗矩陣中循環移位參數的選取

下面討論4環的情況。如果一個LDPC碼含有4環，則它所對應的校驗矩陣中必然有4個“1”處于某個矩形的四個頂點，該環路路徑可表示為：


定理2 按照式(1)所示矩陣分裂方法構造的矩陣所對應的LDPC碼不含長為4的環的充要條件有式(6)成立：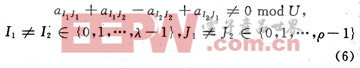


該定理的正確性從前面的描述中即可得知，這里不再贅述。