AES算法中S-box和列混合單元的優(yōu)化及FPGA技術(shù)實現(xiàn)
(2)GF[(24)2]到GF(28)的逆映射。構(gòu)造線性變換T-1,GF(24)上的逆p,q映射到GF(28)上的逆元素y,如式(10)所示。其中,線性變換T-1和乘法求遞步驟(1)中的線性變換T滿足:TT-1=E。

(3)通過域GF(24)上的運算,求b,C的逆p,q。首先構(gòu)建GF(24),q(x)=x4+x+1作為域GF(24)上的本源多項式,a(x),d(x),e(x)∈GF(24)。其中,a(x)=a3x3+a2x2+a1x+a0,d(x)=d3x3+d2x2+d1x+d0,e(x)=e3x3+e2x2+e1x+e0定義域GF(24)上的加法、乘法、逆運算。
①加法為按位異或。
②乘法為多項式相乘后用q(x)取模,按公式e(x)=a(x)d(x)mod q(x)進行運算;
③求逆根據(jù)公式公式a?a-1=1 mod q(x),計算GF(24)上元素a的逆a-1;
構(gòu)造GF(24)上的一次多項式bx+c,并利用上述GF(24)上的加法、乘法和求逆運算進行運算,得到GF(24)上的元素b,c的逆p,q,由式(7)可得:
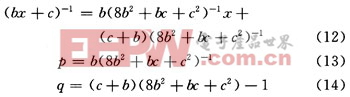
p,q的計算是S-box中最復(fù)雜的邏輯運算,占用了大量的邏輯關(guān)系,關(guān)于p,q的分量元素計算是由上述算法中的分量元素代入式(13)、式(14)求得。
在這種設(shè)計方案中,求逆運算模塊中所選用的即約多項式p(x)和本源多項式q(x)不同,減低了求逆模塊的復(fù)雜度。根據(jù)理論分析,本文中用到的p(x)和q(x)不會減低AES算法的安全性。
2 列混合單元的優(yōu)化設(shè)計
在列混合(MixColumn)和逆列混合(InvMixColumn)的操作中,由以下兩式定義了兩個主要操作:

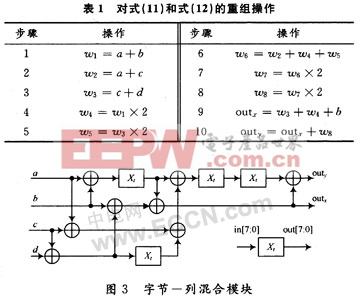
將式(15)和式(16)所做的操作及結(jié)果列于表1中,由步驟1~步驟5處理的結(jié)果得到outx,接著由outx和w8得到outy。因此,在執(zhí)行過程中,操作所用到的硬件資源及其所得結(jié)果可以應(yīng)用到步驟9,步驟10中。如圖3所示,這種新型結(jié)構(gòu)(字節(jié)-列混合模塊)僅需8個加法器和4個乘法器。與原方案相比,此設(shè)計大大減少了硬件復(fù)雜度并顯著節(jié)省了資源的消耗。












評論